武汉市黄陂区2015届九年级上10月联考数学试题及答案

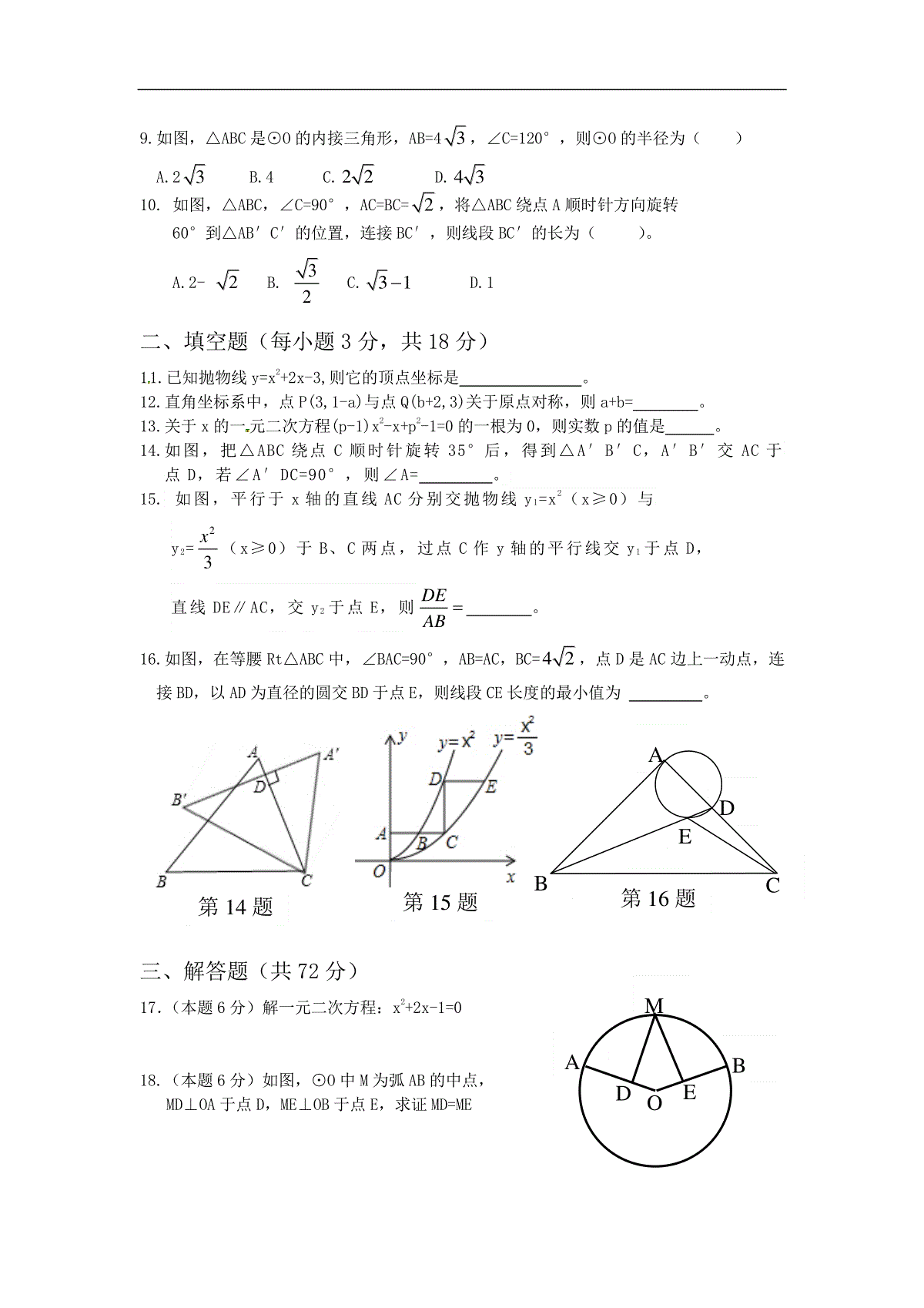
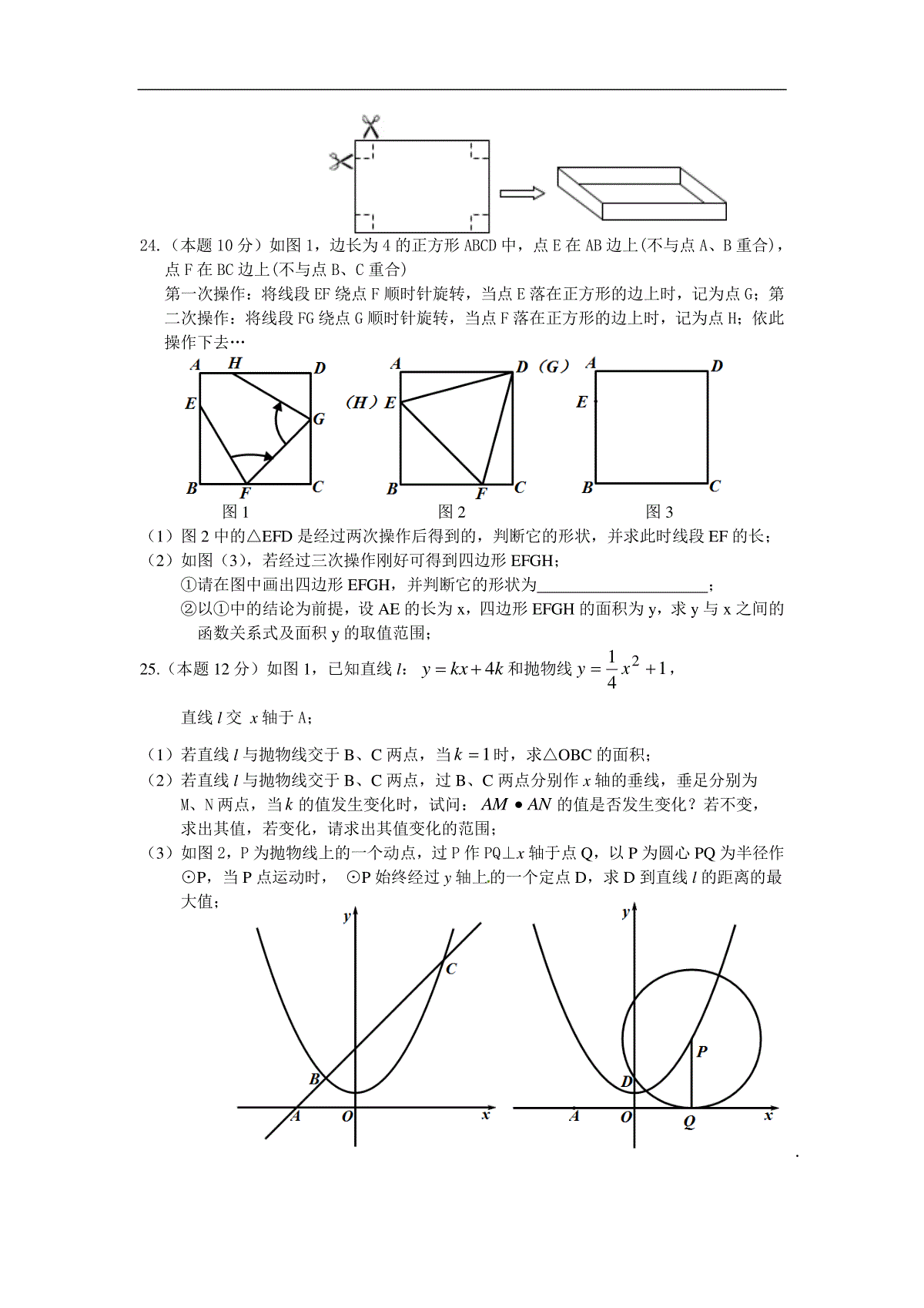
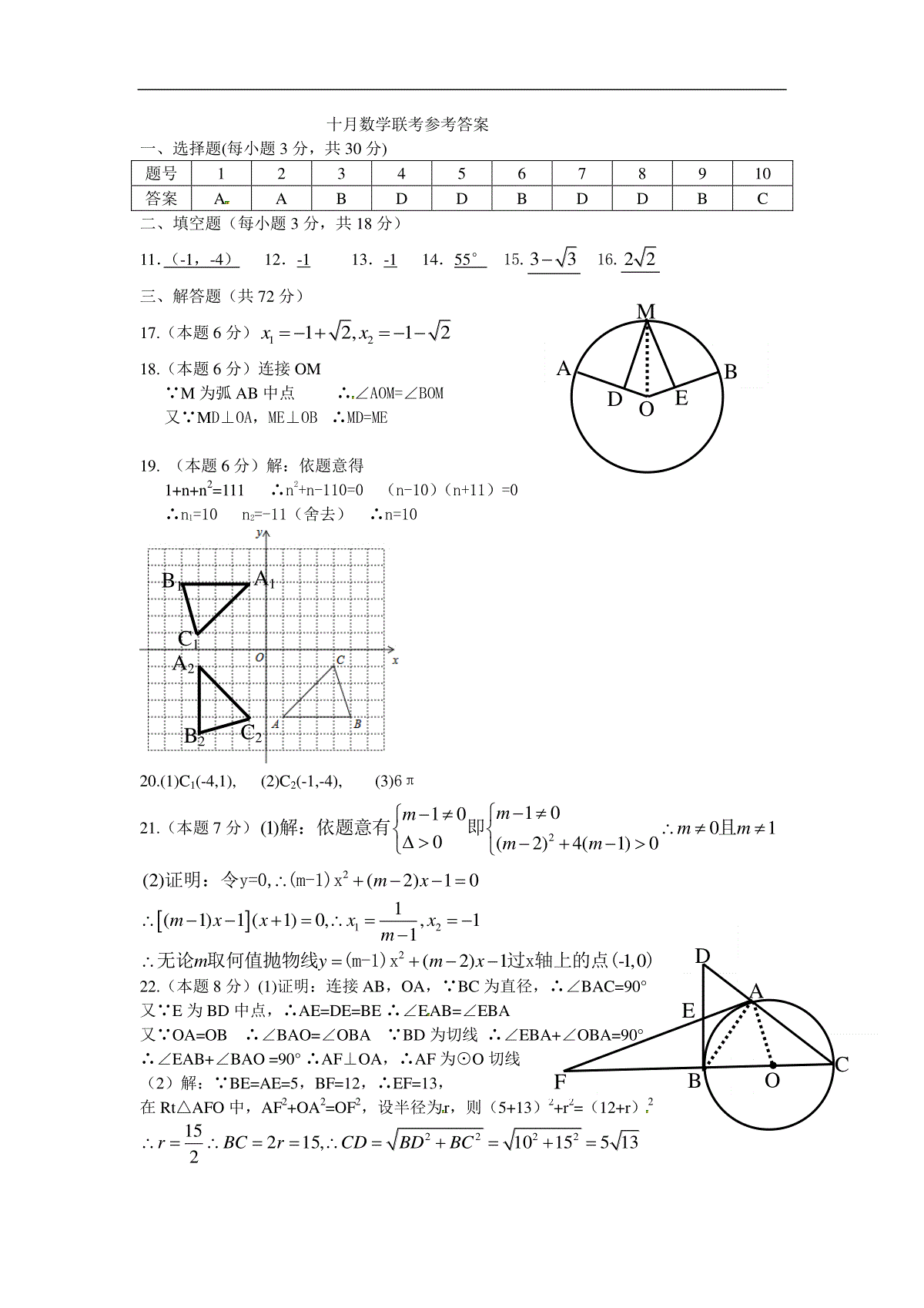
部分学校九年级十月联考数学试卷一、选择题（每题3分，共30分）1.一元二次方程x2=2x的根为（）A.x1=0,x2=2B.x=±2C.x=0D.x=22.下列电视台的台标，是中心对称图形的是（）A.BC.D.3.设方程x2-3x-1=0的两根分别为x1,x2,则x1+x2=()A.-3B.3C.-1D.14.如图是二次函数y=ax2+bx+c的部分图象，由图象可知不等式ax2+bx+c＜0的解集是（）A.-1＜x＜5B.x＞5C.x＜-1且x＞5D.C.x＜-1或x＞55.如图，PA、PB是⊙O的两条切线，A、B为切点，AC为⊙O的直径，∠P=70°，则∠PBC=（）A.110°B.120ºC.135°D.145°6.在平面直角坐标系中，将抛物线y=2x2向上平移2个单位,所得图象的解析式为（）A.y=2x2-2B.y=2x2+2C.y=2(x-2)2D.y=2(x+2)27.某品牌电脑2009年的销售单价为7200元，由于科技进步和新型电子原材料的开发运用，该品牌电脑成本不断下降，销售单价也逐年下降．至2011年该品牌电脑的销售单价为4900元，设2009年至2010年，2010年至2011年这两年该品牌电脑的销售单价年平均降低率均为x，则可列出的正确的方程为()A．4900（1+x）2=7200B．7200（1-2x）=4900C．7200（1-x）=4900（1+x）D．7200（1-x）2=49008.如图，点A1、A2、A3、…、An在抛物线y=x2图象上，点B1、B2、B3、…、Bn在y轴上，若△A1B0B1、△A2B1B2、…、△AnBn-1Bn都为等腰直角三角形（点B0是坐标原点），则△A2014B2013B2014的腰长等于（）A.2013B.2014C.20132D.20142第8题x520yBCOAP第9题图ABCO第10题B′C′ACB9.如图，△ABC是⊙O的内接三角形，AB=43，∠C=120°，则⊙O的半径为（）A.23B.4C.22D.4310.如图，△ABC，∠C=90°，AC=BC=2，将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置，连接BC′，则线段BC′的长为（）。A.2-2B.32C.31D.1二、填空题（每小题3分，共18分）11.已知抛物线y=x2+2x-3,则它的顶点坐标是。12.直角坐标系中，点P(3,1-a)与点Q(b+2,3)关于原点对称，则a+b=。13.关于x的一元二次方程(p-1)x2-x+p2-1=0的一根为0，则实数p的值是。14.如图，把△ABC绕点C顺时针旋转35°后，得到△A′B′C，A′B′交AC于点D，若∠A′DC=90°，则∠A=。15.如图，平行于x轴的直线AC分别交抛物线y1=x2（x≥0）与y2=23x（x≥0）于B、C两点，过点C作y轴的平行线交y1于点D，直线DE∥AC，交y2于点E，则DEAB。16.如图，在等腰Rt△ABC中，∠BAC=90°，AB=AC，BC=42，点D是AC边上一动点，连接BD，以AD为直径的圆交BD于点E，则线段CE长度的最小值为。三、解答题（共72分）17．（本题6分）解一元二次方程：x2+2x-1=018.（本题6分）如图，⊙O中M为弧AB的中点，MD⊥OA于点D，ME⊥OB于点E，求证MD=ME第14题第16题CBEDA第15题ADOEBM19.（本题6分）为了宣传环保，小明写了一篇倡议书，决定用微博转发的方式传播，他设计了如下的传播规则：将倡议书发表在自己的微博上，再邀请n个好友转发倡议书，每个好友转发倡议书之后，又邀请n个互不相同的好友转发倡议书，依此类推，已知经过两轮传播后，共有111人参与了传播活动，求n的值是多少？20.（本题7分）如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点C坐标为（4，-1）．(1)已知△ABC与△A1B1C1关于原点O对称，请在图中画出△A1B1C1，并直接写出C点的对称点C1的坐标为；(2)以原点O为旋转中心，将△ABC顺时针旋转90°，得到△A2B2C2，请在图中画出△A2B2C2，并直接写出C点的对称点C2的坐标为；(3)在(2)中的旋转过程中，请直接写出线段AB扫过的面积为。21.（本题7分）已知关于x的一元二次方程(m-1)x2+(m-2)x-1=0(1)若方程有两个不相等的实数根，求m的取值范围；(2)在(1)的条件下，求证：无论m取何值，抛物线y=(m-1)x2+(m-2)x-1总过x轴上的一个固定点。22.（本题8分）如图，A是以BC为直径的⊙O上一点，过点B作⊙O的切线，与CA的延长线相交于点D，E是BD的中点，延长AE与CB的延长线相交于点F。(1)求证AF是⊙O的切线；(2)若BE=5，BF=12，求CD的长。23.（本题10分）如图，把一张长10cm，宽8cm的矩形硬纸板的四周各剪去一个大小一样的正方形，再折成一个无盖的长方体盒子（纸板的厚度忽略不计）．从美观的角度考虑要求底面的短边与长边．．．．．的比不小于23，设四周小正方形的边长为xcm(1)求盒子的侧面积S侧与x的函数关系式，并求x的取值范围。(2)求当正方形的边长x为何值时侧面积S侧最大，并求最大值。(3)若要求侧面积不小于28cm2，直接写出正方形的边长x的取值范围为。第22题EFBOCAD24.（本题10分）如图1，边长为4的正方形ABCD中，点E在AB边上(不与点A、B重合)，点F在BC边上(不与点B、C重合)第一次操作：将线段EF绕点F顺时针旋转，当点E落在正方形的边上时，记为点G；第二次操作：将线段FG绕点G顺时针旋转，当点F落在正方形的边上时，记为点H；依此操作下去…图1图2图3（1）图2中的△EFD是经过两次操作后得到的，判断它的形状，并求此时线段EF的长；（2）如图（3），若经过三次操作刚好可得到四边形EFGH；①请在图中画出四边形EFGH，并判断它的形状为；②以①中的结论为前提，设AE的长为x，四边形EFGH的面积为y，求y与x之间的函数关系式及面积y的取值范围；25.（本题12分）如图1，已知直线l：kkxy4和抛物线1412xy，直线l交x轴于A；（1）若直线l与抛物线交于B、C两点，当1k时，求△OBC的面积；（2）若直线l与抛物线交于B、C两点，过B、C两点分别作x轴的垂线，垂足分别为M、N两点，当k的值发生变化时，试问：ANAM的值是否发生变化？若不变，求出其值，若变化，请求出其值变化的范围；（3）如图2，P为抛物线上的一个动点，过P作PQ⊥x轴于点Q，以P为圆心PQ为半径作⊙P，当P点运动时，⊙P始终经过y轴上的一个定点D，求D到直线l的距离的最大值；十月数学联考参考答案一、选择题(每小题3分，共30分)题号12345678910答案AABDDBDDBC二、填空题（每小题3分，共18分）11．（-1，-4）12．-113．-114．55°15.3316.22三、解答题（共72分）17.（本题6分）1212,12xx18.（本题6分）连接OM∵M为弧AB中点∴∠AOM=∠BOM又∵MD⊥OA，ME⊥OB∴MD=ME19.（本题6分）解：依题意得1+n+n2=111∴n2+n-110=0（n-10）（n+11）=0∴n1=10n2=-11（舍去）∴n=1020.(1)C1(-4,1),(2)C2(-1,-4),(3)6π21.（本题7分）21010(1)010(2)4(1)0mmmmmm解：依题意有即且22.（本题8分）(1)证明：连接AB，OA，∵BC为直径，∴∠BAC=90°又∵E为BD中点，∴AE=DE=BE∴∠EAB=∠EBA又∵OA=OB∴∠BAO=∠OBA∵BD为切线∴∠EBA+∠OBA=90°∴∠EAB+∠BAO=90°∴AF⊥OA，∴AF为⊙O切线（2）解：∵BE=AE=5，BF=12，∴EF=13，在Rt△AFO中，AF2+OA2=OF2，设半径为r，则（5+13）2+r2=（12+r）2222215215,10155132rBCrCDBDBCADOEBMA1B1C1A2B2C22122(2)(2)101(1)1(1)0,,11(2)1-1,0mxmxxxxmmymx证明：令y=0,(m-1)x无论取何值抛物线(m-1)x过x轴上的点()EFBOCAD23.（本题10分）(1)S=2（10-2x）x+2(8-2x)x=-8x2+36x822,2,820,4102324xxxxxx又229819(2)8368()04247(3)22SxxxaSxSx有最大值，当时，有最大值24.（本题10分）(1)△EFD是等边三角形，易证△AED≌△CFD∴CF=AE，设AE=x∴BE=4-x∴EF=222(4),4xDEx222(4)4843484324(843)4642xxxxxEF(2)解如图所示EFGH为正方形（3）y=SABCD-4S△AEH=16-4×0.5×x（4-x）=2（x-2）2+8∴816y25.（本题12分）（1）∵k=1∴l为y=x+424B-2,2,(6,10)114yxCyx由得（）,E(0,4)11114246162222OBCOEBOECBCSSSOExOEx(2)2241140,4,4(14)1414BCBCykxkxkxkxxkxxkyx由得4A-4,0AMAN=(4)(4)4()16BCBCBCykxkxxxxxx由得（）=4(1-4k)+4×4k+16=20(3)21P(t,1),PFyFPD4t设作轴于，连2222222211FD===(1)=144PDPFPQPFttt2211OD=OF1(1)2,(0,2),2544FDttDAD∵直线l是绕点A旋转，d≤DA∴当DA⊥l时D到l的距离最大25最大值是FGHEF