九年级上册数学测试题及答案

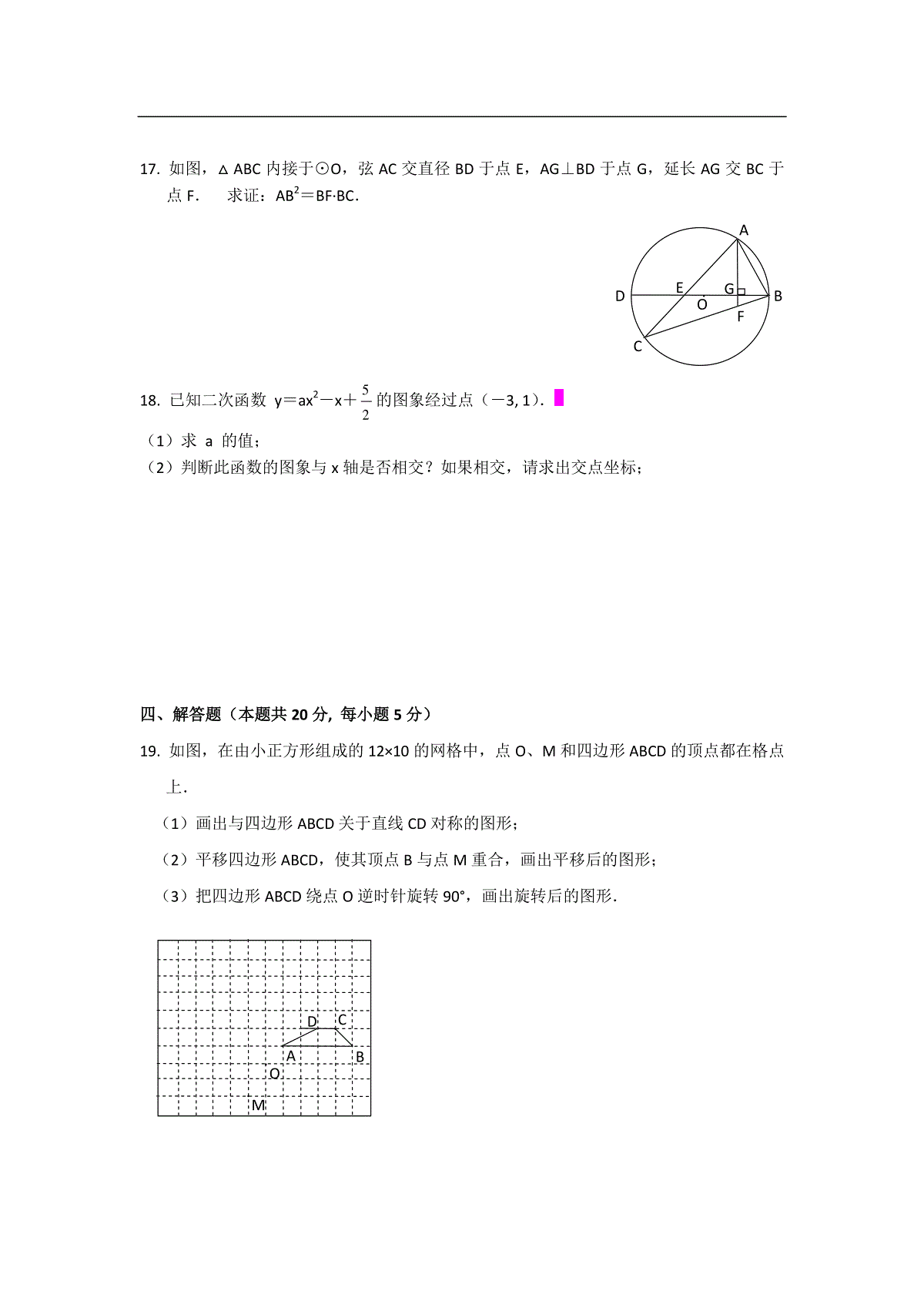
一、选择题（在下列各题的四个备选答案中，只有一个是符合题意的，请将正确答案前的字母写在答题纸上；本题共32分，每小题4分）1.已知⊙O的直径为3cm，点P到圆心O的距离OP＝2cm，则点PA.在⊙O外B.在⊙O上C.在⊙O内D.不能确定2.已知△ABC中，∠C=90°，AC=6，BC=8，则cosB的值是A．0.6B．0.75C．0.8D．343．如图，△ABC中，点M、N分别在两边AB、AC上，MN∥BC，则下列比例式中，不正确的是A.B.C.D.4.下列图形中，既是中心对称图形又是轴对称图形的是A．B.C.D.5.已知⊙O1、⊙O2的半径分别是1cm、4cm，O1O2=10cm，则⊙O1和⊙O2的位置关系是A．外离B．外切C．内切D．相交6.某二次函数y=ax2+bx+c的图象如图所示，则下列结论正确的是A.a0,b0,c0B.a0,b0,c0C.a0,b0,c0D.a0,b0,c07．下列命题中，正确的是A．平面上三个点确定一个圆B．等弧所对的圆周角相等C．平分弦的直径垂直于这条弦D．与某圆一条半径垂直的直线是该圆的切线8.把抛物线y＝－x2＋4x－3先向左平移3个单位，再向下平移2个单位，则变换后的抛物线解析式是A．y＝－(x＋3)2－2B．y＝－(x＋1)2－1C．y＝－x2＋x－5D．前三个答案都不正确二、填空题（本题共16分,每小题4分）9．已知两个相似三角形面积的比是2∶1，则它们周长的比_____.ACNMByxO10．在反比例函数y＝x1k中，当x＞0时，y随x的增大而增大，则k的取值范围是_________.11.水平相当的甲乙两人进行羽毛球比赛，规定三局两胜，则甲队战胜乙队的概率是_________；甲队以2∶0战胜乙队的概率是________．12．已知⊙O的直径AB为6cm，弦CD与AB相交，夹角为30°，交点M恰好为AB的一个三等分点，则CD的长为_________cm．三、解答题（本题共30分,每小题5分）13.计算：cos245°－2tan45°＋tan30°－3sin60°．14.已知正方形MNPQ内接于△ABC（如图所示），若△ABC的面积为9cm2，BC＝6cm，求该正方形的边长．15.某商场准备改善原有自动楼梯的安全性能，把倾斜角由原来的30°减至25°（如图所示），已知原楼梯坡面AB的长为12米，调整后的楼梯所占地面CD有多长？（结果精确到0.1米；参考数据：sin25°≈0.42，cos25°≈0.91，tan25°≈0.47）16．已知：△ABC中，∠A是锐角，b、c分别是∠B、∠C的对边．求证：△ABC的面积S△ABC＝21bcsinA．AMQBNPCACDB30°17.如图，△ABC内接于⊙O，弦AC交直径BD于点E，AG⊥BD于点G，延长AG交BC于点F．求证：AB2＝BF·BC．18.已知二次函数y＝ax2－x＋25的图象经过点（－3,1）．（1）求a的值；（2）判断此函数的图象与x轴是否相交？如果相交，请求出交点坐标；四、解答题（本题共20分,每小题5分）19.如图，在由小正方形组成的12×10的网格中，点O、M和四边形ABCD的顶点都在格点上．（1）画出与四边形ABCD关于直线CD对称的图形；（2）平移四边形ABCD，使其顶点B与点M重合，画出平移后的图形；（3）把四边形ABCD绕点O逆时针旋转90°，画出旋转后的图形．ABC·DEFGOABDCOM······20.口袋里有5枚除颜色外都相同的棋子，其中3枚是红色的，其余为黑色．（1）从口袋中随机摸出一枚棋子，摸到黑色棋子的概率是_______；（2）从口袋中一次摸出两枚棋子，求颜色不同的概率．（需写出“列表”或画“树状图”的过程）21.已知函数y1＝－31x2和反比例函数y2的图象有一个交点是A（a，－1）．（1）求函数y2的解析式；（2）在同一直角坐标系中，画出函数y1和y2的图象草图；（3）借助图象回答：当自变量x在什么范围内取值时，对于x的同一个值，都有y1＜y2？22.工厂有一批长3dm、宽2dm的矩形铁片，为了利用这批材料，在每一块上裁下一个最大的圆铁片⊙O1之后（如图所示），再在剩余铁片上裁下一个充分大的圆铁片⊙O2．（1）求⊙O1、⊙O2的半径r1、r2的长；（2）能否在剩余的铁片上再裁出一个与⊙O2同样大小的圆铁片？为什么？A·BCD1O1五、解答题（本题共22分,第23、24题各7分，第25题8分）23．如图，在△ABC中，AB＝AC，以AB为直径的⊙O分别交AC、BC于点M、N，在AC的延长线上取点P，使∠CBP＝21∠A．（1）判断直线BP与⊙O的位置关系，并证明你的结论；（2）若⊙O的半径为1，tan∠CBP＝0.5，求BC和BP的长．24.已知：如图，正方形纸片ABCD的边长是4，点M、N分别在两边AB和CD上（其中点N不与点C重合），沿直线MN折叠该纸片，点B恰好落在AD边上点E处．（1）设AE＝x，四边形AMND的面积为S，求S关于x的函数解析式，并指明该函数的定义域；（2）当AM为何值时，四边形AMND的面积最大？最大值是多少？ABPCNMO·EBCCMNAD·25.在直角坐标系xOy中，已知某二次函数的图象经过A（－4，0）、B（0，－3），与x轴的正半轴相交于点C，若△AOB∽△BOC（相似比不为1）．（1）求这个二次函数的解析式；（2）求△ABC的外接圆半径r；（3）在线段AC上是否存在点M（m，0），使得以线段BM为直径的圆与线段AB交于N点，且以点O、A、N为顶点的三角形是等腰三角形？若存在，求出m的值；若不存在，请说明理由．一、ACCBDABB二、9.2：110.k-111.21,4112.35三、13.原式=2)22(-2+33-3×23=21-2+33-23……………………………………4分=-3+33……………………………………………………5分14.作AE⊥BC于E，交MQ于F.由题意，21BC×AE=9cm2，BC=6cm.∴AE=3cm.……………………………1分设MQ=xcm，∵MQ∥BC，∴△AMQ∽△ABC.……………………2分∴AEAFBCMQ.……………………3分又∵EF=MN=MQ，∴AF=3-x.∴3x-36x.……………………………………4分解得x=2.答：正方形的边长是2cm.…………………………5分15.由题意，在Rt△ABC中，AC=21AB=6（米）,…………………1分又∵在Rt△ACD中，∠D=25°，CDAC=tan∠D,……………………………3分∴CD=tan256≈47.06≈12.8（米）.答：调整后的楼梯所占地面CD长约为12.8米.……………………5分16.证明：作CD⊥AB于D，则S△ABC=21AB×CD.………………2分∵不论点D落在射线AB的什么位置，在Rt△ACD中，都有CD=ACsinA.…………………4分又∵AC=b，AB=c，∴S△ABC=21AB×ACsinACADBAMFQBNEPCADBCHEGOF=21bcsinA.…………5分17.证明：延长AF，交⊙O于H.∵直径BD⊥AH，∴AB⌒=BH⌒.……………………2分∴∠C=∠BAF.………………………3分在△ABF和△CBA中，∵∠BAF=∠C，∠ABF=∠CBA，∴△ABF∽△CBA.…………………………………………4分∴ABBFCBAB，即AB2=BF×BC.…………………………………………5分证明2：连结AD，∵BD是直径，∴∠BAG+∠DAG=90°.……………………1分∵ＡＧ⊥ＢＤ，∴∠DAG+∠D=90°.∴∠BAF=∠BAG=∠D.……………………2分又∵∠C=∠D，∴∠BAF=∠C.………………………3分……18.⑴把点（-3，1）代入，得9a+3+25=1，∴a=-21.⑵相交……………………………………………2分由-21x2-x+25=0，……………………………3分得x=-1±6.∴交点坐标是（-1±6，0）.……………………………4分⑶酌情给分……………………………………………5分19.给第⑴小题分配1分，第⑵、⑶小题各分配2分.20.⑴0.4……………………………………………2分⑵0.6……………………………………………4分列表（或画树状图）正确……………………………………5分21.⑴把点A（a，-1）代入y1=-2x31，得–1=-a31，∴a=3.……………………………………………1分ADBCEGOF设y2=xk，把点A（3，-1）代入，得k=–3，∴y2=–x3.……………………………………2分⑵画图；……………………………………3分⑶由图象知：当x0,或x3时，y1y2.……………………………………5分22.⑴如图，矩形ABCD中，AB=2r1=2dm，即r1=1dm.………………………………1分BC=3dm，⊙O2应与⊙O1及BC、CD都相切.连结O1O2，过O1作直线O1E∥AB，过O2作直线O2E∥BC，则O1E⊥O2E.在Rt△O1O2E中，O1O2=r1+r2，O1E=r1–r2，O2E=BC–(r1+r2).由O1O22=O1E2+O2E2，即（1+r2)2=(1–r2)2+(2–r2)2.解得，r2=4±23.又∵r22,∴r1=1dm，r2=（4–23）dm.………………3分⑵不能.…………………………………………4分∵r2=（4–23）4–2×1.75=21(dm),即r221dm.，又∵CD=2dm，∴CD4r2，故不能再裁出所要求的圆铁片.…………………………………5分23.⑴相切.…………………………………………1分证明：连结AN，∵AB是直径，∴∠ANB=90°.∵AB=AC，∴∠BAN=21∠A=∠CBP.又∵∠BAN+∠ABN=180°-∠ANB=90°，∴∠CBP+∠ABN=90°，即AB⊥BP.∵AB是⊙O的直径，yy2oxA(3,-1)y1=-2x31y2ADBCO1EO2AMBNCDPO∴直线BP与⊙O相切.…………………………………………3分⑵∵在Rt△ABN中，AB=2，tan∠BAN=tan∠CBP=0.5，可求得，BN=52，∴BC=54.…………………………………………4分作CD⊥BP于D，则CD∥AB，ABCDAPCP.在Rt△BCD中，易求得CD=54，BD=58.…………………………………5分代入上式，得2CPCP=52.∴CP=34.…………………………………………6分∴DP=1516CDCP22.∴BP=BD+DP=58+1516=38.…………………………………………7分24.⑴依题意，点B和E关于MN对称，则ME=MB=4-AM.再由AM2+AE2=ME2=(4-AM)2，得AM=2-2x81.……………………1分作MF⊥DN于F，则MF=AB，且∠BMF=90°.∵MN⊥BE，∴∠ABE=90°-∠BMN.又∵∠FMN=∠BMF-∠BMN=90°-∠BMN，∴∠FMN=∠ABE.∴Rt△FMN≌Rt△ABE.∴FN=AE=x，DN=DF+FN=AM+x=2-2x81+x.………………………2分∴S=21(AM+DN)×AD=(2-2x81+2x)×4=-2x21+2x+8.……………………………3分其中，0≤x＜4.………………………………4分⑵∵S=-2x21+2x+8=-21(x-2)2+10,∴当x=2时，S最大=10；…………………………………………5分此时，AM=2-81×22=1.5………………………………………6分答：当AM=1.5时，四边形AMND的面积最大，为10.⑶不能，0＜AM≤2.…………………………………………7分AEDMFNBC25.⑴∵△AOB∽△BOC（相似比不为1），∴OAOBOBOC.又∵OA=4,OB=3,∴OC=32×41=49.∴点C(49,0).…………………1分设图象经过A、B、C三点的函数解析式是y=ax2+bx+c,则c=-3，且