raptor软件使用

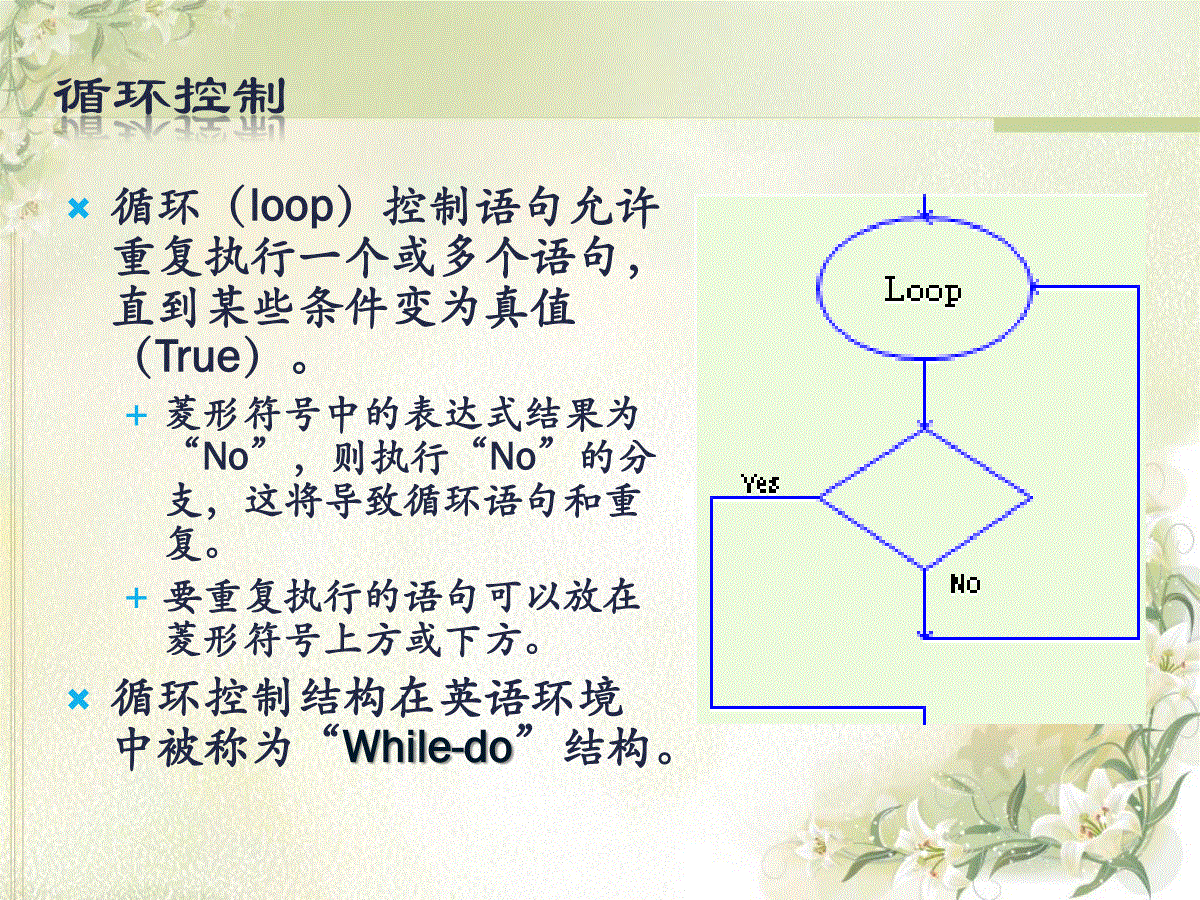
RAPTOR程序设计基础《可视化计算》循环控制循环（loop）控制语句允许重复执行一个或多个语句，直到某些条件变为真值（True）。菱形符号中的表达式结果为“No”，则执行“No”的分支，这将导致循环语句和重复。要重复执行的语句可以放在菱形符号上方或下方。循环控制结构在英语环境中被称为“While-do”结构。典型的循环错误未修改Count的值Count的值永远为1Count的值永远不会等于-100计数控制循环之一求一个正整数的累加。计数控制循环之二一张纸折几下可以比珠穆朗玛峰高。（0.5mm，8848m）RAPTOR子程序的定义与调用在计算机科学中，将实际问题抽象化是解决问题的关键要素之一。为了解决复杂的问题，必须能够研究问题的“主要方面（bigissues）”。组合数求解很容易看到，求组合数需要多次求阶乘，这会造成许多重复的代码。可以将求阶乘代码独立出主程序，定义为一个子程序，在主程序运行时，需要计算某数的阶乘时就调用子程序，从而简化整个软件的组成，使结构更清晰。子程序子程序如同一个加工厂，输入原材料，然后按设计要求处理原材料，输出产成品。子程序的原材料就是一些变量,例如（in:m）,为统计子程序输入测试样本。子程序的产成品也是变量，例如（out:s）,向调用它的程序返回统计结果。其中，in,out表示子程序的输入输出参数。创建RAPTOR子程序点击“模式”菜单，选择“中级”。•在“main”上点鼠标右键，选择“增加一个子程序”。子程序定义子程序定义的参数称为“形式参数”。RAPTOR的子程序参数不得超过6个。子程序参数可以是单个变量，也可以是数组。求阶乘的子程序过程调用语句在“main”或其它子程序中添加过程调用语句。双击定义该语句。JC(m,m1)实参子程序的调用如要调用子程序，可以通过调用语句并给子程序的接口赋予“实际参数”进行。实际参数的名与形式参数的可以不同。实际参数的数据类型则必须与形式参数的相同。五、算法示例1．迭代算法（递推法）让计算机对一组指令进行重复执行，在每次执行这组指令时，都从变量的原值推出它的一个新值。在数学中，迭代经常被用来进行数值计算，累加与累乘问题是最典型、最基本的一类算法，实际应用中很多问题都可以归结为累加与累乘问题。累加：S=0inputnForj=1tons=s+j累乘：F=1inputnFork=1tonF=F*k具体方法是：如左图：先给一个近似根的一个初值x1，过A点(f(x1))作切线交x轴于x2点。实际上是找出x2,再由x2找出x3,x4…，直到满足精度为10-6的根(解)。由点斜式方程得斜率k：【例】求一元高次方程2x3-4x2+3x-6=0在x=1.5附近的近似根，要求精度为10-6。分析：“迭代法”又称“递推法”，其基本思想是把一个复杂的计算过程简化为简单过称的多次重复。每次的重复都是从旧值的基础上递推出新值，直至满足精度要求。11xxyykf’(x1)=0-f(x1)/(x2-x1)x2=x1-f(x1)/f’(x1)得递推公式：xn+1=xn–f(xn)/f’(xn)本题中，我们用f表示f(xn)，f1表示f’(xn)634223nnnxxxf38621nnxxf19k=y’=f’(x)A点初的切线在x轴上的x2处有y2=0而【思考题】小猴有桃若干，第一天吃掉一半多一个；第二天吃剩下桃子的一半多一个；以后每天都吃尚存桃子的一半多一个，到第7天要吃时只剩一个，问小猴原有桃多少？分析：也是递推(迭代)问题。用后一天的数推出前一天的桃子数。设第n天的桃子为xn，是前一天的桃子的二分之一减去1。121即：1nnxx?；求2)1(也就是：01xxxnn01；求2)1(xxxnn2．穷举算法穷举法也叫枚举法，是对众多可能解，通过多重循环一一列举出该问题所有可能的解，并在逐一列举的过程中，检验每个可能的解是否是问题的真正解，若是，就采用这个解，否则抛弃它。穷举的计算量是相当大的，但对于计算机来说，做起来很容易。采用穷举法解题的基本思想：（1）明确问题要求，确定枚举对象，用合适类型的变量表示枚举对象。（2）明确枚举对象的取值范围。（3）根据题目要求，写出有关的条件表达式。这里条件表达式可以是数学表达式、关系表达式或逻辑表达式。（4）用循环语句枚举出可能的解，在循环体内验证各种条件表达式是否满足。（5）根据问题背景，优化程序，以便缩小搜索范围，减少程序运行时间。例1：从1~10中找出所有是3倍数的数。用流程图描述解决此数学问题的算法如右图所示。例2：百元买百鸡。公鸡5块钱一只，母鸡三块钱一只、小鸡一块钱三只，编程求解购鸡方案。分析：(1)设母鸡、公鸡、小鸡的数量各为x、y、z，列出方程为：x+y+z=1005x+3y+z/3=100三个未知数，两个方程，此题有若干个整数解。(2)计算机求解此类问题，采用试凑法(也称穷举法)来实现，即将可能出现的各种情况一一罗列测试，判断是否满足条件，采用循环结构来实现。11233．排序算法排序（Sort），就是将一组数据元素按照某个关键字递增或递减的次序排列起来。选择法排序：找出表中关键字最小的元素，将其与第一个元素进行交换，再在其余元素中找出关键字最小的元素，将其与第二个元素进行交换。依次类推，直到将表中所有关键字按由小到大的顺序排列好为止。选择法排序Fori=1To5Step1Min=a(i)Forj=i+1To6Step1IfMina(j)ThenMin=a(j)p=jEndIfNextjn=a(i)a(i)=a(p)a(p)=nNextiVB程序段冒泡法排序：从第一个开始，对数组中两两相邻的元素比较，值较小的放在前面，值较大的放在后面，一轮比较完毕，一个最大的数沉底成为数组中的最后一个元素，一些较小的数如同气泡一样上浮一个位置。n个数，经过n-1轮比较后完成排序。a(1)a(2)a(3)a(4)a(5)a(6)第1轮比较683279a(1)a(2)a(3)a(4)a(5)第2轮比较632789a(1)a(2)a(3)a(4)第3轮比较326789a(1)a(2)a(3)第4轮比较236789a(1)a(2)第5轮比较236789原始数据869327a(1)a(2)a(3)a(4)a(5)a(6)4.递归算法：程序调用自身的编程技巧称为递归（recursion）。一个过程或函数在其定义或说明中又直接或间接调用自身的一种方法，它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解，递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算，大大地减少了程序的代码量。注意：(1)递归就是在过程或函数里调用自身;(2)在使用递增归策略时，必须有一个明确的递归结束条件，称为递归出口。递归的原理，其实就是使用栈(stack).栈是限定在一端进行插入和删除的线性表。栈是按照“先进后出”或者“后进先出”的原则组织数据的。入栈出栈栈顶栈底A1A2An…栈示意图例1：递归法求N!【解题】递归过程在自身定义的内部调用自己，fac(n)=n!的递归函数：1)1fac(*11)fac(nnnnn进栈出栈当n=4时，求解过程：Functionfac(nAsInteger)AsLongIfn=1Thenfac=1Elsefac=n*fac(n-1)EndIfEndFunction递归函数程序段：例2：汉诺塔问题源于印度一个古老传说。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定：在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。不论白天黑夜，总有一个僧侣在按照上面的法则移动这些金片。僧侣们预言，当所有的金片都从梵天穿好的那根柱上移到另外一根柱上时，世界就将在一声霹雳中消灭，而梵塔、庙宇和众生也都将同归于尽。如果考虑一下把64片金片，由一根针上移到另一根针上，并且始终保持上小下大的顺序。这需要多少次移动呢?这里需要递归的方法。原柱x辅助柱y目标柱z三个盘子汉诺塔问题的递归求解示意图如下图所示。34原柱x辅助柱y目标柱z四个盘子汉诺塔问题的递归求解示意图如下图所示。5．查找算法查找是根据给定的某个“值”，在查找表中确定一个其关键字等于给定“值”的数据元素，若表中存在称此查找是成功的。若表中不存在称此查找不成功的。顺序查找插入数据基本思想是：1）首先查找待插入数据在数组中的位置k；2）然后从最后一个元素开始往前直到下标为k的元素依次往后移动一个位置；3)第k个元素的位置腾出，将数据插入。147101316192225④③②①14kx删除数据基本思想是：a)删除操作首先也是要找到欲删除的元素的位置k；b)然后从k+1到n个位置开始向前移动；c)最后将数组元素减1。14710131416192225①②③④⑤k