当前位置:首页 > 商业/管理/HR > 公司方案 > 数列通项公式的十种方法(已打)
1递推式求数列通项公式常见类型及解法对于由递推式所确定的数列通项公式问题,通常可通过对递推式的变形转化成等差数列或等比数列,也可以通过构8造把问题转化。下面分类说明。一、型例1.在数列{an}中,已知,求通项公式。解:已知递推式化为,即,所以。将以上个式子相加,得,2所以。二、型例2.求数列的通项公式。解:当,即当,所以。3三、型例3.在数列中,,求。解法1:设,对比,得。于是,得,以3为公比的等比数列。所以有。解法2:又已知递推式,得上述两式相减,得,因此,数列是以为首项,以3为公比的等比数列。所以,所以。4四、型例4.设数列,求通项公式。解:设,则,,所以,即。设这时,所以。由于{bn}是以3为首项,以为公比的等比数列,所以有。由此得:。说明:通过引入一些尚待确定的系数转化命题结构,经过变形与比较,把问题转化成基本数列(等差或等比数列)。5五、型例5.已知b≠0,b≠±1,,写出用n和b表示an的通项公式。解:将已知递推式两边乘以,得,又设,于是,原递推式化为,仿类型三,可解得,故。说明:对于递推式,可两边除以,得,引入辅助数列,然后可归结为类型三。6六、型例6.已知数列,求。解:在两边减去。所以为首项,以。所以令上式,再把这个等式累加,得。所以。说明:可以变形为,就是,则可从,解得,于是是公比为的等比数列,这样就转化为前面的类型五。等差、等比数列是两类最基本的数列,是数列部分的重点,自然也是高考考查的热点,而考查的目的在于测试灵活运用知识的能力,这个“灵活”往往集中在“转化”的水平上。转化的目的是化陌生为熟悉,当然首先是等差、等比数列,根据不同的递推公式,采用相应的变形手段,达到转化的目的。7附:构建新数列巧解递推数列竞赛题递推数列是国内外数学竞赛命题的“热点”之一,由于题目灵活多变,答题难度较大。本文利用构建新数列的统一方法解答此类问题,基本思路是根据题设提供的信息,构建新的数列,建立新数列与原数列对应项之间的关系,然后通过研究新数列达到问题解决之目的。其中,怎样构造新数列是答题关键。1求通项求通项是递推数列竞赛题的常见题型,这类问题可通过构建新数列进行代换,使递推关系式简化,这样就把原数列变形转化为等差数列、等比数列和线性数列等容易处理的数列,使问题由难变易,所用的即换元和化归的思想。例1、数列na中,11a,nnnaaa241411611。求na。(1981年第22届IMO预选题)分析本题的难点是已知递推关系式中的na241较难处理,可构建新数列nb,令nnab241,这样就巧妙地去掉了根式,便于化简变形。解:构建新数列nb,使0241nnab则51b,nnab2412,即2412nnbannnbbb24141161241221化简得22132nnbb321nnbb,即32131nnbb数列3nb是以2为首项,21为公比的等比数列。nnnb2122123即322nnb121122231232241nnnnnba2证明不等式这类题一般先通过构建新数列求出通项,然后证明不等式或者对递推关系式先进行巧妙变形后再构建新数列,然后根据已经简化的新数列满足的关系式证明不等式。例2、设10a,12111nnnaaaNn,求证:22nna。(1990年匈牙利数学奥林匹克试题)8分析利用待证的不等式中含有及递推关系式中含有211na这两个信息,考虑进行三角代换,构建新数列n,使nntga,化简递推关系式。证明:易知0na,构建新数列n,使nntga,2,0n则2sincos111111112nnnnnntgtgtga21nntgtg,21nn又10a,8121tga,从而81因此,新数列n是以8为首项,21为公比的等比数列。212821nnn考虑到当)2,0(x时,有xtgx。所以,2222nnntga注:对型如21na,na1,111nnnnaaaa都可采用三角代换。3证明是整数这类题把递推数列与数论知识结合在一起,我们可以根据题目中的信息,构建新数列,找到新的递推关系式直接解决,或者再进行转化,结合数论知识解决。例3、设数列na满足11a,nnnaaa1211)(Nn求证:Nan2221,nNn。分析直接令222nnab,转化为证明Nbn)1,(nNn证明:构建新数列nb,令0222nnab则2422nnba,242121nnba9代入221121nnnaaa整理得222124nnnbbb从而2121224nnnbbb)3(n于是2212121221122424nnnnnnbbbbbb)3(n12211nnnbbb)3(n由已知,42b,243b,由上式可知,Nb4,Nb5,依次类推,Nbn)1(n,即Nan222。例4、设r为正整数,定义数列na如下:11a,2)1(221nnnaarnn)(Nn求证:Nan。(1992年中国台北数学奥林匹克试题)分析把条件变形为rnnnnaan21122比较1na与na前的系数及1na与na的足码,考虑到另一项为rn212,等式两边同乘以1n,容易想到构新数列nb,使nnannb1。证明:由已知得rnnnnaan2112212112121rnnnannann构建新数列nb,nnannb1则21b,12112rnnnbb1111nkkknbbbb1212123212rrrnNbn11121212)(2nkrrrnknknb112212212212211212122nkrrrrrrrrrknCknCknCnnnbn10又nkrrnknkrrnknkknkb112121112121)1(nkrrrrrrrrknCknCknCn1221221221221121211111n|nb1nn|nb,从而Nan。4解决整除问题一般通过构建新数列求出通项,再结合数论知识解决,也可用数学归纳法直接证明。例5、设数列na满足11a,32a,对一切Nn,有nnnanana2312,求所有被11整除的na的一切n值。(1990年巴尔干地区数学奥林匹克试题)分析变形递推关系式为nnnnaanaa1122,就容易想到怎样构建新数列了。解:由已知nnnnaanaa1122构建新数列,2nbnnnnaab111n则22b,nnnnbnaanb11112n!311221nbnnbnnnbbnnn2nnknkknknnnkbaaaa12211!1从而3114a,4203118a,3670831110a,当11n时,由于101!kk被11整除,因而nkknkka11101!!也被11整除。所以,所求n值为4n,8,及10n的一切自然数。5证明是完全平方数这类题初看似乎难以入手,但如能通过构建新数列求出通项na,问题也就迎刃而解了。11例6、设数列na和nb满足10a,00b,且47836711nnnnnnbabbaa,2,1,0n求证:na是完全平方数。(2000年全国高中联赛加试题)分析先用代入法消去nb和1nb,得061412nnnaaa,如果等式中没有常数项6,就可以利用特征根方法求通项,因此可令aaCnn,易求得21a。证明:由①式得nb,1nb代入②得061412nnnaaa化为02121142112nnnaaa构建新数列nc,21nnac,且210c,2721367210011baac01412nnnccc由特征方程01142得两根3471,3472所以nnnmmc2211当0n,1时,有21347347212121mmmm解得:4121mm则nnnc3474134741①②12nn2232413241则232324121nnnnca因为nn3232为正偶数,所以,na是完全平方数。从上述各题构建新数列的过程中,可以看出对题设中递推式的观察、分析,并据其结构特点进行合理变形,是成功构建新数列的关键。构建新数列的目的是为了化繁为简、化未知为已知、化不熟悉为熟悉,这也是解答数学问题的共性之所在。

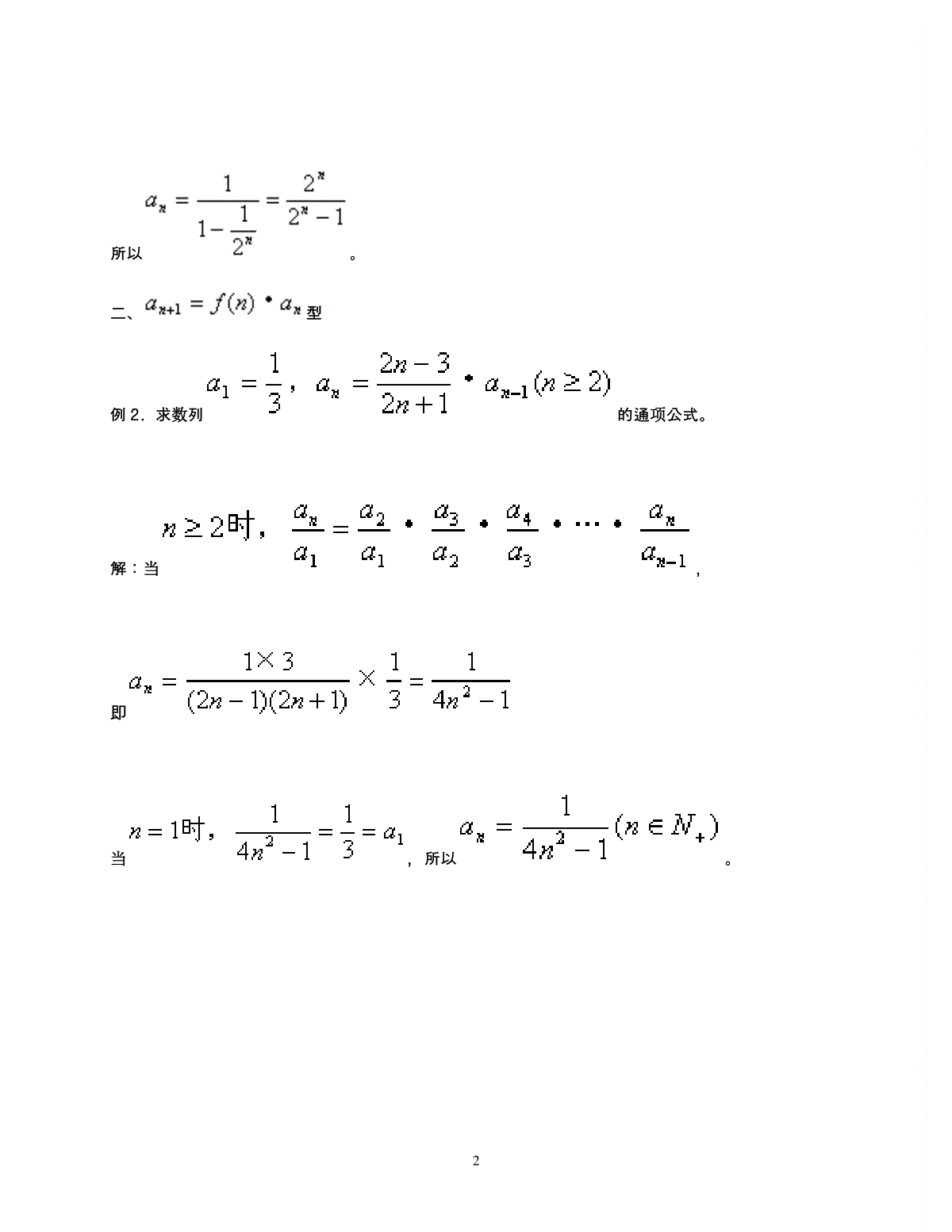


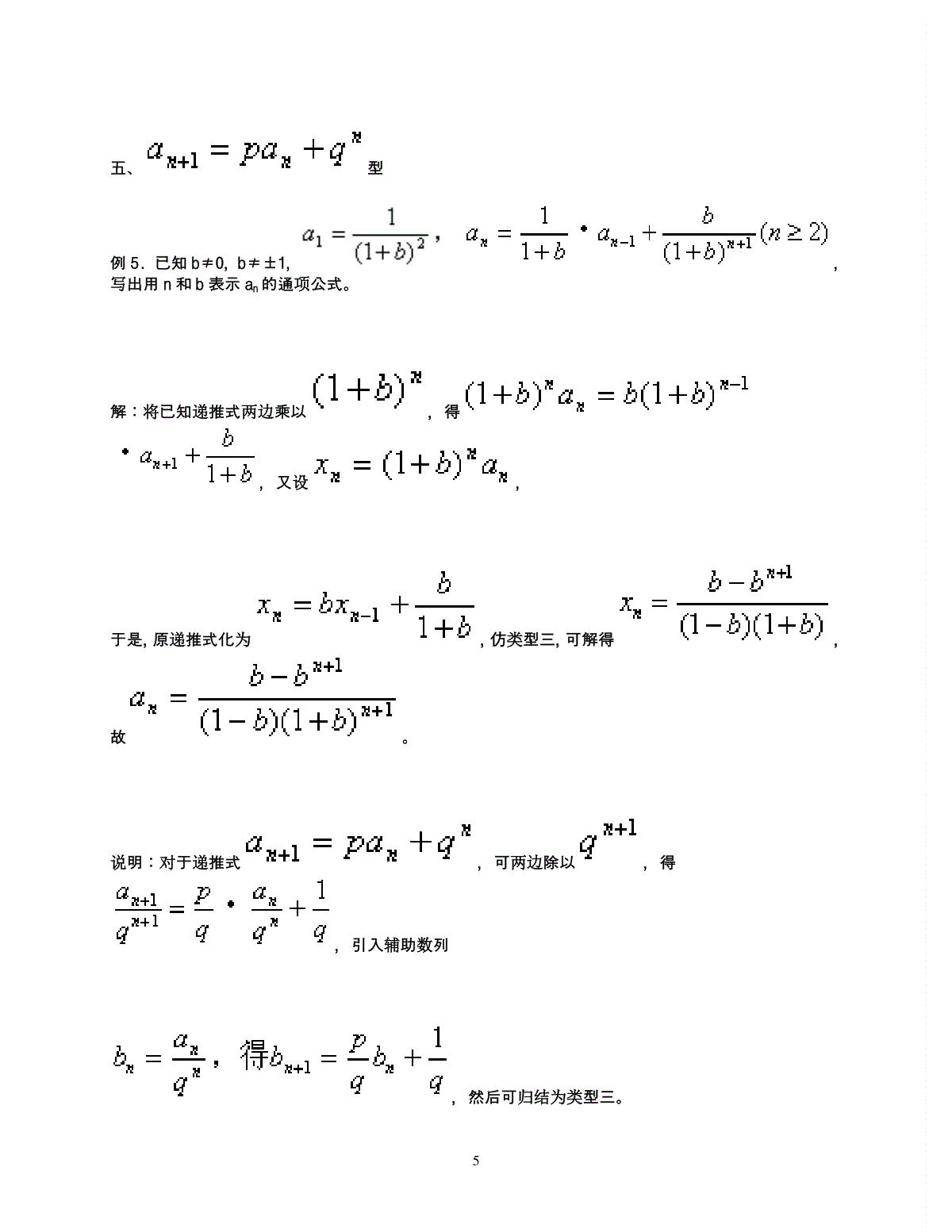
 三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
本文标题:数列通项公式的十种方法(已打)
链接地址:https://www.777doc.com/doc-5567315 .html