当前位置:首页 > 中学教育 > 高中教育 > 高二数学第二学期期末考试模拟卷
海量资源尽在星星文库:高二数学第二学期期末考试模拟卷数学试题一、选择题(本大题共8小题,每小题5分,计40分)1.设34)1(6)1(4)1(234xxxxS,则S等于(A)A.x4B.x4+1C.(x-2)4D.x4+42.从1,2,…,9这九个数中,随机抽取3个不同的数,则这3个数的和为偶数的概率是(C)A.95B.94C.2111D.21103.已知自由落体运动的速率gtv,则落体运动从0t到0tt所走的路程为(C)A.320gtB.20gtC.220gtD.620gt4.若nxx)13(3)(Nn展开式中含有常数项,则n的最小值是(A)A.4B.3C.12D.105.设随机变量~(0,1)N,记)()(xPx,则(11)P等于(A)A.2(1)1B.2(1)1C.(1)(1)2D.(1)(1)6.如果复数ZaiZ322满足条件||,那么实数a的取值范围是(D)A.(,)2222B.(,)22C.(,)11D.(,)337.已知复数ZabiZbaiab12,(其中、都是实数,且ab0),在复平面内,Z1、Z2所对应的点与原点组成的三角形是(C)A.锐角三角形B.直角三角形C.等腰直角三角形D.等边三角形8.在下列四个命题中:①已知A、B、C、D是空间的任意四点,则0DACDBCAB;②若{cba,,}为空间的一组基底,则{accbba,,}也构成空间的一组基底;③|||||||)(|cbacba;④对于空间的任意一点O和不共线的三点A、B、C,若海量资源尽在星星文库:(其中Rzyx,,),则P、A、B、C四点共面.其中正确的个数是(B)A.3B.2C.1D.0二、填空题(本大题共6小题,每小题5分,计30分)9.若以连续投掷两次骰子分别得到的点数m、n作为点P的坐标,则点P落在直线x+y=5下方的概率是61奎屯王新敞新疆10.已知△ABC,A(1,1),B(2,3),C(3,-1),在矩阵21212121作用所得到的图形围成的面积是___________.11.设)()11()11()(Nniiiinfnn,则集合)(nfxx中元素的个数是3.12.曲线1,0,2yxxy,所围成的图形的面积可用定积分表示为dxx102)1(.13.已知3412M,1314N,则满足方程NMX的二阶方阵X=1512914.如图,已知命题:若矩形ABCD的对角线BD与边AB和BC所成角分别为、,则,1coscos22若把它推广到长方体ABCD—A1B1C1D1中,试写出相应命题形式:若长方体ABCD-A1B1C1D1的对角线BD1与BA1,BB1,BC所成的角分别为,,,则1coscoscos222。.DCBAD1C1CDABA1B1海量资源尽在星星文库:三、解答题(共90分)15.设虚数z1,z2,满足221zz.(1)若z1,z2又是一个实系数一元二次方程的两根,求z1,z2.(2)若z1=1+mi(i为虚数单位,m∈R),2||1z,复数w=z2+3,求|w|的取值范围.解:(1)∵z1,z2是一个实系数一元二次方程的两个虚根,因此必共轭,可设z1=a+bi(a,b∈R且b≠0),则z2=a-bi,由221zz得(a+bi)2=a-bi即:a2-b2+2abi=a-bi根据复数相等,bababa222∵b≠0解得:2321ba或2321ba,∴iziz2321232121或iziz2321232121.(2)由于221zz,z1=1+mi,w=z2+3,∴w=(1+mi)2+3=4-m2+2mi.∴12)2(4)4(||22222mmmw,由于2|z|1且m≠0,可解得0m2≤1,令m2=u,12)2(||2uw,在u∈(0,1)上,(u-2)2+12是减函数,∴)4,13[||w.16.函数数列)(xfn满足:)0(1)(21xxxxf,)]([)(11xffxfnn(1)求)(),(32xfxf;(2)猜想)(xfn的表达式,并证明你的结论。海量资源尽在星星文库:解:⑴221111221)(1)())(()(xxxfxfxffxf…………2’222221331)(1)())(()(xxxfxfxffxf…………2’⑵猜想:)(1)(2Nnnxxxfn……………………3’下面用数学归纳法证明:①当n=1时,211)(xxxf,已知,显然成立………………1’②假设当)(NKKn时,猜想成立,即21)(kxxxfk则当1Kn时,2222211)1(1)1(11)(1)())(()(xkxkxxkxxxfxfxffxfkkkk……3’即对1Kn时,猜想也成立。结合①②可知:猜想21)(nxxxfn对一切Nn都成立。………………2’17.设有编号为1,2,3,4,5的五个球和编号为1,2,3,4,5的五个盒子,现将这五个球放入5个盒子内.(1)只有一个盒子空着,共有多少种投放方法?(2)没有一个盒子空着,但球的编号与盒子编号不全相同,有多少种投放方法?(3)每个盒子内投放一球,并且至少有两个球的编号与盒子编号是相同的,有多少种投放方法?解:(1)C52A54=1200(种)……4分(2)A55-1=119(种)……8分海量资源尽在星星文库:(3)满足的情形:第一类,五个球的编号与盒子编号全同的放法:1种第二类,四个球的编号与盒子编号相同的放法:0种第三类,三个球的编号与盒子编号相同的放法:10种第四类,二个球的编号与盒子编号相同的放法:2C52=20种∴满足条件的放法数为:1+10+20=31(种)……14分18.如图,正方体ABCD-A1B1C1D1中,点E是棱BC的中点,点F是棱CD上的动点.(Ⅰ)试确定点F的位置,使得D1E⊥平面AB1F;(Ⅱ)当D1E⊥平面AB1F时,求二面角C1―EF―A的余弦值以及BA1与面C1EF所成的角的大小.解:(1)以A为原点,直线AB、AD、AA1为x轴、y轴、z轴建立空间直角坐标系,不妨设正方体的棱长为1,且xDF,则)0,1,0(),0,0,1(),000()1,0,0(1DBAA,,,)0,1,(),0,21,1()1,1,0(),1,0,1(11xFEDB于是)0,1,(),1,0,1(),1,21,1(11xAFABED由AFEDABEDFABED11111且面于是00111AFEDABED与,可解得21x所以当点F是CD的中点时,FABED11平面(2)当FABED11平面时,F是CD的中点,)0,1,21(F平面AEF的一个法向量为)1,0,0(m而在平面C1EF中,)0,21,21(),1,21,0(1EFEC所以平面C1EF的一个法向量为)1,2,2(n31,cosnm,31arccos,nm又因为当把m,n都移向这个二面角内一点时,m背向平面AEF,而n指向平面C1EF故二面角C1―EF―A的大小为31arccosD1C1B1A1DCBAEF海量资源尽在星星文库:又)1,0,1(1BA,nBA,cos122,所以01135,nBABA1与平面C1EF所成的角的大小为045.19.在一个盒子中,放有标号分别为1,2,3的三张卡片,现从这个盒子中,有放回...地先后抽得两张卡片的标号分别为x、y,记xyx2.(Ⅰ)求随机变量的最大值,并求事件“取得最大值”的概率;(Ⅱ)求随机变量的分布列和数学期望.解:(Ⅰ)x、y可能的取值为1、2、3,12x,2xy,3,且当3,1yx或1,3yx时,3因此,随机变量的最大值为3.有放回抽两张卡片的所有情况有933种,92)3(P.答:随机变量的最大值为3,事件“取得最大值”的概率为92.(Ⅱ)的所有取值为3,2,1,0.0时,只有2,2yx这一种情况,1时,有1,1yx或1,2yx或3,2yx或3,3yx四种情况,2时,有2,1yx或2,3yx两种情况.91)0(P,94)1(P,92)2(P.则随机变量的分布列为:0123P91949292海量资源尽在星星文库:因此,数学期望914923922941910E.20.当兔子和狐狸处于同一栖息地时,忽略其他因素,只考虑兔子数量和狐狸数量的相互影响,为了简便起见,不妨做如下假设:(1)由于自然繁殖,兔子数每年增长10%,狐狸数每年减少15%;(2)由于狐狸吃兔子,兔子数每年减少狐狸数的0.15倍,狐狸数每年增加兔子数的0.1倍;(3)第n年时,兔子数量nR用表示,狐狸数量用nF表示;(4)初始时刻(即第0年),兔子数量有1000R只,狐狸数量有300F只。请用所学知识解决如下问题:(1)列出兔子与狐狸的生态模型;(2)求出nR、nF关于n的关系式;(3)讨论当n越来越大时,兔子与狐狸的数量是否能达到一个稳定的平衡状态,说明你的理由。解:⑴)1(85.01.015.01.11111nFRFFRRnnnnnn……………………4’⑵设nnnFR,1.01.1M85.015.0∴)(21nnnMMM=……=nM又矩阵M的特征多项式1.01.1)(f85.015.0=)95.0)(1(95.095.12令0)(f得:95.0,121特征值11对应的一个特征向量为231特征值95.02对应的一个特征向量为112……………………6’海量资源尽在星星文库:∴2211011070nnnnM=nnn95.011014095.01102101195.01102370∴nnnnFR95.011014095.0110210………………………………14’⑶当n越来越大时,n95.0越来越接近于0,nR,nF分别趋向于常量210,140。即随着时间的增加,兔子与狐狸的数量逐渐增加,当时间充分长后,兔子与狐狸的数量达到一个稳定的平衡状态。……2’


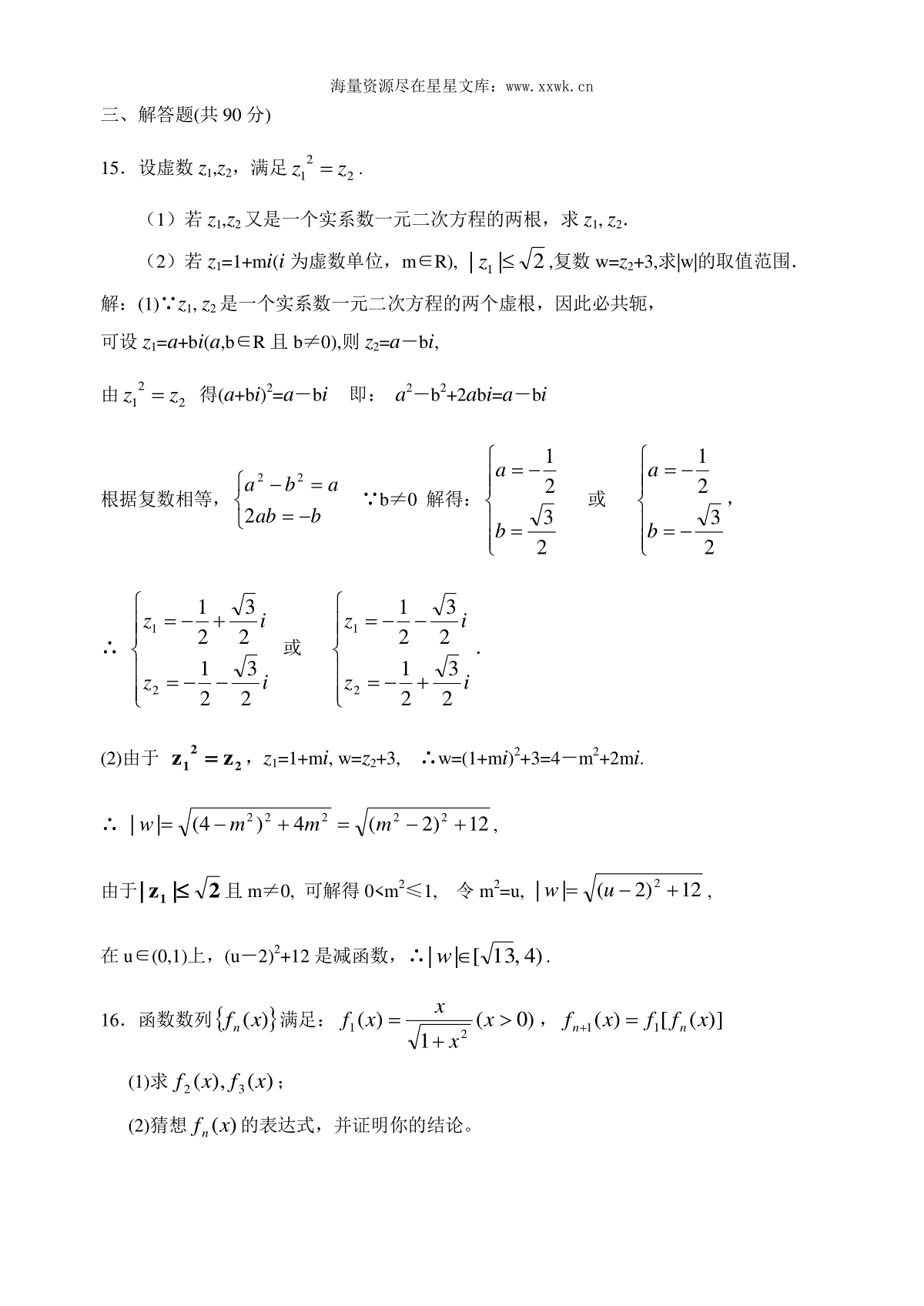


 三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
本文标题:高二数学第二学期期末考试模拟卷
链接地址:https://www.777doc.com/doc-5785244 .html