决策理论与方法第五章多属性决策、多目标及序贯决策

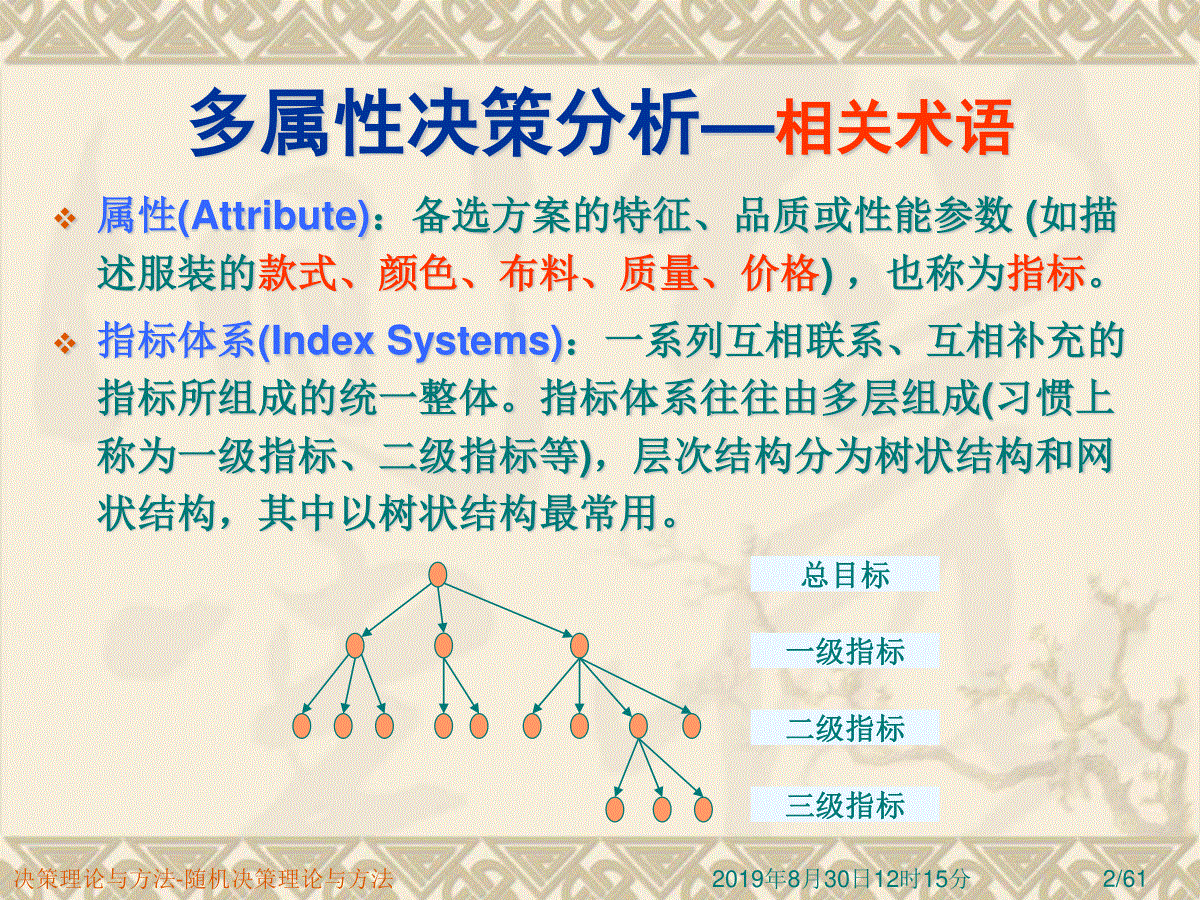
2019年8月30日12时15分决策理论与方法-随机决策理论与方法1/61多属性决策分析—多目标决策什么是多目标决策问题？(例如购买衣服时，款式、价格、颜色、质量等可能都是决策目标)。多目标决策问题的特点：决策问题的目标多于一个；多个目标间不可公度(non-commensurable)，即各目标没有统一的衡量标准，难以比较；各目标之间存在矛盾。一般将决策变量离散、决策方案有限的多目标决策问题称为多属性(Multi-attribute)决策问题；而将决策变量连续、有无限决策方案的多目标决策问题称为多目标(Multi-objective)决策问题。两者又可以统称为多准则(Multi-criterion)决策问题。2019年8月30日12时15分决策理论与方法-随机决策理论与方法2/61多属性决策分析—相关术语属性(Attribute)：备选方案的特征、品质或性能参数(如描述服装的款式、颜色、布料、质量、价格)，也称为指标。指标体系(IndexSystems)：一系列互相联系、互相补充的指标所组成的统一整体。指标体系往往由多层组成(习惯上称为一级指标、二级指标等)，层次结构分为树状结构和网状结构，其中以树状结构最常用。一级指标总目标二级指标三级指标2019年8月30日12时15分决策理论与方法-随机决策理论与方法3/61多属性决策分析—相关术语目标(Objective)：决策人的愿望或决策人所希望达到的、努力的方向(如物美价廉)。在多目标决策中，目标是求极值的对象，是需要优化的函数式。目的(Goal)：在特定时间、空间状态下，决策人的期望，是目标的具体数值表现。目标和目的常混用。准则(Criterion)：判断的标准或度量事物价值的原则及检验事物合意性的规则，兼指属性和目标。2019年8月30日12时15分决策理论与方法-随机决策理论与方法4/61多属性决策分析—求解过程引发调查研究和改变系统必要性分析明确问题、标明目标、辨识属性构造模型、估计参数方案集X属性值f(x)评价或优化决策实施或重新评价价值判断决策环境自然状态一、启动二、构造问题三、系统建模四、分析评价五、决策与实施2019年8月30日12时15分决策理论与方法-随机决策理论与方法5/61多属性决策分析—目标与属性在多目标决策中，决策目标常用目标集、目标递阶分层结构以及属性集描述；目标递阶分层结构的最下层目标要用一个或多个属性来描述；不同的方案对应的各属性值存在差异，也就导致目标实现的差异，因此可借此来评价方案的优劣；替代属性：某些目标无法用属性值直接度量时，需要使用替代属性对目标进行度量。如师资队伍的质量可以用学历结构、职称结构、专业结构、科研能力等替代属性来衡量。(寻找“替代属性/替代变量”在科学研究中是非常重要的)2019年8月30日12时15分决策理论与方法-随机决策理论与方法6/61多属性决策分析—目标与属性属性选择的要求：每个属性是可测和可理解的；属性集是最小完备集：既要能够描述决策问题的所有(重要)方面，又不能有冗余；属性的测量值是可运算的；属性集内的各属性相互独立、可分解。但在实际决策中，上述要求很难达到，这也正是我们开展决策理论与方法研究的动力源。2019年8月30日12时15分决策理论与方法-随机决策理论与方法7/61多属性决策分析—目标与属性例：某流域水资源项目建设目标(指标体系)及属性总体目标：提高流域内人民生活水平促进经济发展改善环境质量利用水力资源增加农业生产发展航运改进水质水土保持改善旅游条件保护生态环境防止洪涝灾害发电量作物产量船运量COD水流失土流失景点数动物品种植物品种减灾面积目标递阶分层属性空间2019年8月30日12时15分决策理论与方法-随机决策理论与方法8/61多属性决策分析—问题的符号表示MA=X,A,Θ,V,,fX表示方案集，X={x1,x2,…,xm}A表示属性集，A={a1,a2,…,an}Θ表示状态集，Θ={1,2,…,k}V表示值集，所有可能取值的集合:Θ→V，分布函数，确定各状态发生的可能性f:X×A→V，目标函数，确定各方案对应的属性值2019年8月30日12时15分决策理论与方法-随机决策理论与方法9/61多属性决策分析—问题的符号表示例：给定自然状态的多属性决策问题方案集发电作物船运COD水流失土流失景点数动物植物减灾x18.945557.2827734115887x27.662476.4768245121354x39.246679.59180339124992019年8月30日12时15分决策理论与方法-随机决策理论与方法10/61多属性决策分析—属性值预处理剩下的问题是我们如何评价方案的优劣。属性值预处理的目标是规范化各属性值，使其能够真正体现方案优劣的实际价值。属性值类型：效益型指标：属性值越大越好；成本型指标：属性值越小越好；中性指标：属性值取某一个恰当的值最优，过大、过小都不合适。2019年8月30日12时15分决策理论与方法-随机决策理论与方法11/61多属性决策分析—属性值预处理预处理主要有两项任务：非量纲化：通过某种方法消除量纲的选用对决策或评价结果的影响。归一化：不同属性的属性值取值范围存在很大差别，为了真实反映各属性值的价值，需要将属性值统一变换到[0,1]区间上以消除属性取值范围的差异对决策或评价结果的影响。2019年8月30日12时15分决策理论与方法-随机决策理论与方法12/61多属性决策分析—属性值预处理设fi(a)为方案i的a属性值，记fmax=max(fi(a))，fmin=min(fi(a))线性变换效益型。变换z:fi(a)→zi(a)定义为：zi(a)=fi(a)/fmax；成本型。变换z:fi(a)→zi(a)定义为：zi(a)=1-fi(a)/fmax；或者变换z:fi(a)→zi(a)定义为：zi(a)=fmin/fi(a)。标准0-1变换效益型。zi(a)=(fi(a)-fmin)/(fmax-fmin)；成本型。zi(a)=(fmax-fi(a))/(fmax-fmin)。向量规范化：zi(a)=fi(a)/(ifin(a))1/n(n可以取1或2)。2019年8月30日12时15分决策理论与方法-随机决策理论与方法13/61多属性决策分析—属性值预处理ji人均论著(a1)科研经费(a3)逾期毕业率(a4)10.00001.00000.000020.03700.78800.714230.18520.20700.485740.07410.57590.228651.00000.05681.0000ji人均论著(a1)科研经费(a3)逾期毕业率(a4)逾期毕业率(a4)10.03571.00000.00000.255320.07140.80000.53190.545530.21430.25200.36170.400040.10710.60000.17020.307751.00000.05680.74471.0000ji人均论著(a1)生师比(a2)科研经费(a3)逾期毕业率(a4)10.5550004.721.0740002.233.01012603.041.5430003.9514.022841.2fmax1450004.7fmin0.52841.2(f2)1/214.4471887.25ji人均论著(a1)科研经费(a3)逾期毕业率(a4)10.03460.69560.648220.06930.55650.303430.20780.17530.413740.10390.41740.537850.96950.03950.1655线性变换标准0-1变换向量变换2019年8月30日12时15分决策理论与方法-随机决策理论与方法14/61多属性决策分析—属性值预处理中性属性(最优值为给定区间)规范化策略下极限f0上极限f0最优区间f1～f21zfzi(a)=(1)fi(a)≤f0，0(2)f0fi(a)f1，1-(f1-fi(a))/(f1-f0)(3)f1≤fi(a)≤f2，1(4)f2fi(a)f0，1-(fi(a)-f2)/(f0-f2)(5)fi(a)≥f0，02019年8月30日12时15分决策理论与方法-随机决策理论与方法15/61多属性决策分析—属性值预处理ji生师比(a2)生师比z(a2)设：f0=2,f1=5,f2=6,f0=12151.0000270.83333100.3333440.6666520.0000ji生师比(a2)Temp(a2)生师比z(a2)(1)E=5.6000（均值）(2)Tempi(a)=(fi(a)-E)/E(3)应用线性变换或标准0-1变换或向量变换。本例是采用线性变换。zi(a)=1-tempi(a)/max(tempi(a))150.10710.8636270.25000.68183100.78570.0000440.28570.6364520.64290.18182019年8月30日12时15分决策理论与方法-随机决策理论与方法16/61多属性决策分析—属性值预处理异常(outlier)处理。对同一个属性a，若各方案的值差异极大或某方案的值相对其他方案出现明显的偏离，如按一般方法规范化，在评价时该属性的影响将被不恰当地放大（如前例中的论著一项，方案5的值是14，显著大于其他4个方案）。因此需要采用特别方法处理，处理方法有很多，下面介绍一种常用方法。设定一个转换后的期望值（均值）：M(0.5～0.75)作变换z：fi(a)→zi(a)，zi(a)=(fi(a)-E)×(1-M)/(fmax-E)+M其中E为当前属性值的均值；fmax为当前属性值的最大值2019年8月30日12时15分决策理论与方法-随机决策理论与方法17/61多属性决策分析—属性值预处理0246810121400.10.20.30.40.50.60.70.80.91线性变换M=0.5M=0.6M=0.7M=0.8M=0.9人均论著：AZi(A)异常值处理2019年8月30日12时15分决策理论与方法-随机决策理论与方法18/61多属性决策分析—属性值预处理专家评分范围差异的处理。当一组专家对若干方案进行评价时，由于习惯不同，各自的评分范围可能存在较大差异，需要进行规范化处理。映射区间定义：[M0,M*]定义映射z：fi(a)→zi(a)，zi(a)=M0+(M*-M0)(fi(a)-fmin)/(fmax-fmin)一般取M0=0，M*=1。对应标准0-1转换。2019年8月30日12时15分决策理论与方法-随机决策理论与方法19/61多属性决策分析—属性值预处理两个不同专家对方案1-5评价结果(百分制)如下表。ji专家1(a)专家2(a)专家1(z(a))专家2(z(a))174910.84210.8750265810.36840.4583360700.10530.0000477941.00001.0000558720.00000.08332019年8月30日12时15分决策理论与方法-随机决策理论与方法20/61多属性决策分析—权重确定当决策者面对多个目标时，存在目标的重要性不同的问题，这就需要引入权(Weight)的概念加以解决。权是目标重要性的数量化表示，它的作用有：决策人对目标的重视程度；各目标属性值的差异程度；各目标属性值的可靠程度。权重确定方法：两两比较法。对不同目标的重要性进行两两比较，形成一个判断矩阵。但判断矩阵存在两方面的一致性问题：(1)a1/a2=3,a2/a3=2a1/a3=6?(2)不同专家间的一致性问题a2(1)/a3(1)=2a2(2)/a3(2)=2?2019年8月30日12时15分决策理论与方法-随机决策理论与方法21/61多属性决策分析—权重确定判断矩阵的构造假设属性ai的权记为wi，则wij=wi/wj为判断矩阵A的第i行第j列元素。A