黄建阳一道中考数学压轴题引发的思考

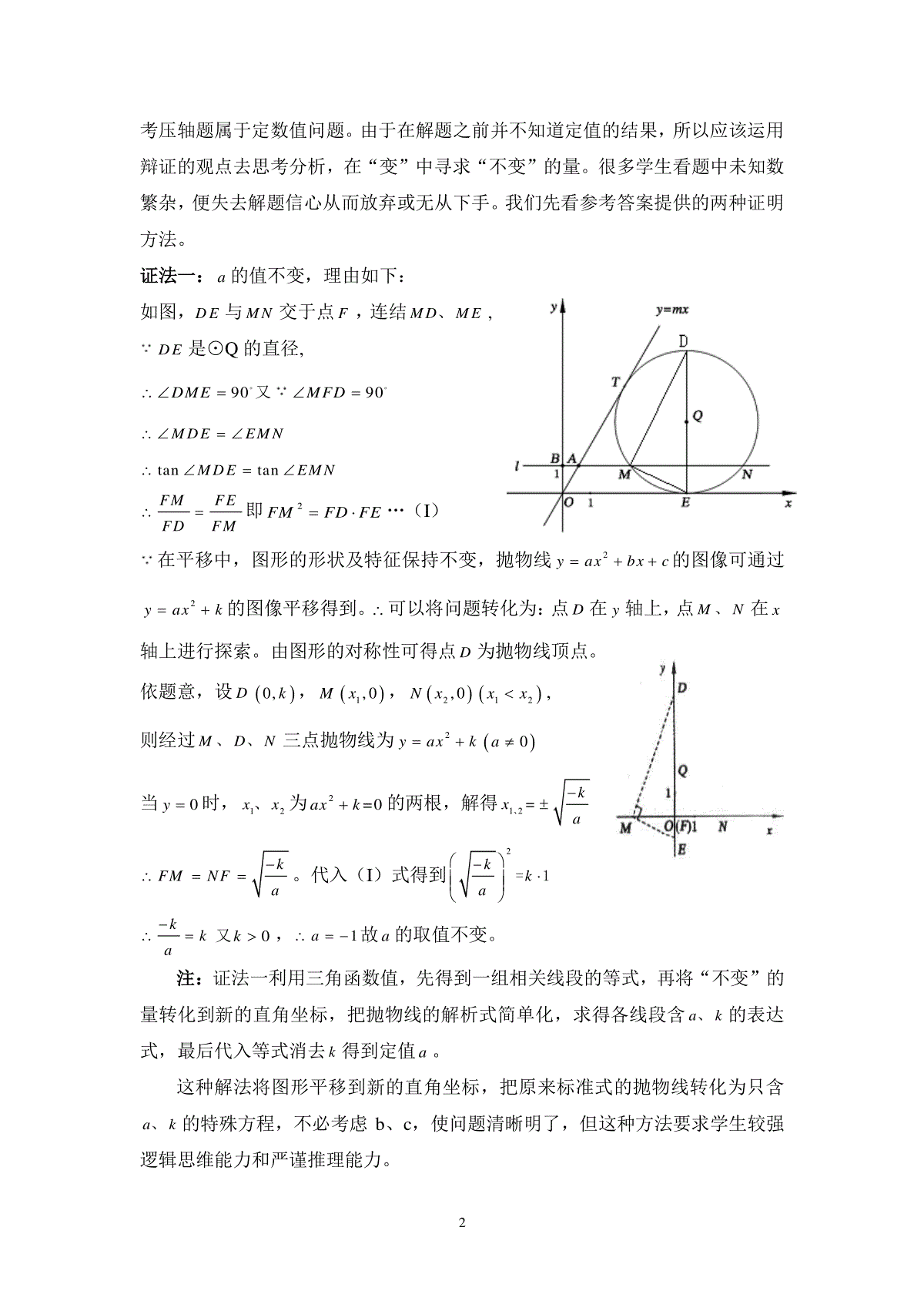
1一道中考数学压轴题引发的思考福建省南安市新侨中学黄建阳摘要：近年来，定值问题的频繁出现已经成了中考压轴题的趋势。在初中阶段，定值问题一直是个难点也是一个重点，它要求学生具有很强的分析能力与综合运用数学知识、数学思想方法解决能力。本文根据近年出现一类中考压轴题结合自己的理解，对这类定值问题的学习进行探究。关键字：中考压轴题、定值、参数一、问题（泉州2011年）：如图，在第一象限内，直线ymx与过点0,1B且平行于x轴的直线l相交于点A，半径为r的⊙Q与直线ymx、x轴分别相切于点TE、,且与直线l分别交于不同的点MN、两点。（1）当点A的坐标为3,3p时，①填空：p=，m=，AOE=；②连结,QTQEQE、交MN于点F,当2r时，试说明：以TMEN、、、为顶点的四边形是等腰梯形；（2）在图1中，连结QE并延长交⊙Q于点D，试探索：对mr、的不同取值，经过MDN、、三点的抛物线2yaxbxc，a的值会变化吗？若不会，求出a的值；若变化，请说明理由。二、证明问题（1）答案略。问题（2）a的取值已经超出义务教育课标的要求：抛物线开口方向[1]。而a大小取决于抛物线的形状。高中教材提到：|a|越大，开口越小；|a|越小,开口越大。近年中考数学注重初高中思维方式的衔接，其中定值问题的出现均是各地中考试卷的一大亮点。所谓定值问题，就是当一部分元素按某种规律在一定范围内变动时，与它有关的某些量始终保持不变，这类问题称为定值问题。定值问题一般分为两类：定量和定形。具体题型又可以分为定点问题、定方向问题、定数值问题等。泉州中2考压轴题属于定数值问题。由于在解题之前并不知道定值的结果，所以应该运用辩证的观点去思考分析，在“变”中寻求“不变”的量。很多学生看题中未知数繁杂，便失去解题信心从而放弃或无从下手。我们先看参考答案提供的两种证明方法。证法一：a的值不变，理由如下：如图，DE与MN交于点F，连结MDME、,DE是⊙Q的直径,9090DMEMFD。。又MDEEMNtantanMDEEMNFMFEFDFM即2FMFDFE…（I）在平移中，图形的形状及特征保持不变，抛物线2yaxbxc的图像可通过2yaxk的图像平移得到。可以将问题转化为：点D在y轴上，点MN、在x轴上进行探索。由图形的对称性可得点D为抛物线顶点。依题意，设D0,k，1,0Mx，2,0Nx12xx,则经过MDN、、三点抛物线为2yaxk0a当0y时，12xx、为2=0axk的两根，解得12=kxa、kFMNFa。代入（I）式得到2kka=1kka0k又，1a故a的取值不变。注：证法一利用三角函数值，先得到一组相关线段的等式，再将“不变”的量转化到新的直角坐标，把抛物线的解析式简单化，求得各线段含ak、的表达式，最后代入等式消去k得到定值a。这种解法将图形平移到新的直角坐标，把原来标准式的抛物线转化为只含ak、的特殊方程，不必考虑b、c，使问题清晰明了，但这种方法要求学生较强逻辑思维能力和严谨推理能力。3证法二：a的取值不变，理由如下：MDF∽EMF得到2FMFDFE…（I），由图形的对称性可得点D为抛物线的顶点，设,Dhk0,21hkr，则1DFk,且抛物线2(0)yaxhka，当1y时，21axhk，解得11=kxha，21=kxha，1112kkkMNhhaaa112kMFNFMNa，代入(I)式得211kka111,1kkka又，1a故a的值不变。注：证法二利用三角形相似得到同证法一相同的线段等式，再将已知二次函数的值代入顶点式得到相关线段的表达式，最后代入等式消去k求得a的定值。证法二较证法一简单，省去证法一中另建直角坐标系，而是巧妙创设抛物线的顶点式，从中省略多余未知数，便求得定值a。证法三：a的取值不变，理由如下：连结QN,设点,0Eh，顶点,Dhk0,21hkr，显然QNF是直角三角形，1,2KQF,2KQN由勾股定理得到：1NFk,从而得到点1,1Nhk。由点1,1Nhk在抛物线2yaxhk过，得到211ahkhk，11,1,akkk又1a故a的值不变。注：证法三利用勾股定理得到含参数hk、的抛物线点坐标，直接将含参数hk、的点坐标代入抛物线顶点式中，借鉴求参数方程，消去参数，便得到定值。在初中，参数在比例线段才有详细介绍，而在《普通高中课程标准》[2]则明确要求参数方程是以参变量为中介来表示曲线上点的坐标的方程，是曲线在同一坐标下又一种表示形式。某些曲线用参数方程表示比用普通方程表示更方便，学习参数方程有助于学生进一步体会解决问题中数学方法的灵活多变。综上三种方法进行比较，证法三运用参数方程思想较为简便，它把复杂的逻辑推理巧妙转化为运算问题，遵循“引参”、“消参”的消参法方进行简便求解。4三、思考定数值问题通常可以通过消参法求解，所谓消参法即在给定的条件下，先引进参数（引参），不必求出其参数数值，再根据已知条件和所学过的知识，将其参数消去（消参），使问题转变了解题途径。1、将原题条件弱化若将点0,1B改为：点0,Bt，其他条件不变，试探索：对mr、的不同取值，经过MDN、、三点的抛物线2yaxbxc，求出a的值。解：利用证法三设点0,Bt，,0Eh，,Dhk0,21hkr，显然QNF是直角三角形，由勾股定理得到：22222kkNFtktt从而得到点2,Nhkttt。由抛物线顶点,Dhk则2yaxhk过点2,Nhkttt，当yt时，22ahktthkt1at。故a是随t的变化而变化。2、条件、结论对换如果已知经过MDN、、三点的抛物线2yaxbxc，对amr、、的不同取值，能否求出点0,Bt中的t值？解法同上，得到1ta，t随a的变化而变化。3、迁移：（黄石市2011年）已知二次函数2248yxmxm（1）当2x时，函数值y随x的增大而减小，求m的取值范围。（2）以抛物线2248yxmxm的顶点A为一个顶点作该抛物线的内接正三角形AMN（M，N两点在抛物线上），请问：△AMN的面积是与m无关的定值吗？若是，请求出这个定值；若不是，请说明理由。分析：2011年黄石市压轴题第二步也是定值问题，正三角形的面积由边长决定，边长大小由抛物线开口大小决定，而|a|越小，开口越大，正三角形的面积越大，xy0ANBM5反之，|a|越大，开口越小，正三角形的面积也越小。因此本题也涉及初高中的衔接思想。类似泉州题型，我们将其进行推广，并运用消参法进行求解。推广：以抛物线2yaxbxc的顶点A为一个顶点作该抛物线的内接正三角形AMN（M，N两点在抛物线上），请问：△AMN的面积是与m的值有关吗？解：令函数2yaxkh，则顶点A,kh，设,Npq，因为点N在抛物线上可得2apkhq……①从而得到ABqh，BNpk∵AMN是正三角形，∴3ABBN，即3qhpk……②，0pk又，由①②可得3pka。22333AMNSABBNBNa，显然△AMN的面积只与a的取值有关，与m的值无关。四、启发数学中考仍是以定量评价全面考察学生数学学习全过程的重要方式。而压轴题不仅注重考察学生对数学概念的理解，数学思想方法的掌握，而且其对数学思考深度，探究与创新的水平及应用数学解决实际问题的能力有更高要求从而发挥甄别与选拔功能。定值问题作为压轴题一直是困扰教师和学生的难点，本文列举今年一类定值问题的中考压轴题进行分析，另辟蹊跷，引入中学一种重要的解题方法——消参法。将较为复杂的逻辑推理，通过引参消参法，使问题转变了解题途径，则问题由难变易而获解。在教学中，将题目进行推广深入探究，体会一些有趣有用的新知识或好方法，使解决数学问题变得简单易懂，从而调动学生积极性，启发学生思维，提高学生的解题能力和探索能力。参考文献：[1]全日制义务教育数学课程标准（实验稿）[S]北京师范大学出版社北京2001年7月第1版34[2]普通高中数学课程标准（实验）[S]人民教育出版社出版北京2003年4月第1次版85.作者：黄建阳、男、1986年6月、汉、福建南安、中学数学、本科、福建南安市新侨中学、,联系电话[phone]、邮箱[e-mail]