蓝园高中高二年数学(理科)矩阵专题练习1.(2009福建理科高考)已知矩阵M2311所对应的线性变换把点A(x,y)变成点A`(13,5),试求M的逆矩阵及点A的坐标2.(2010福建理科高考)已知矩阵1Mb1a,0cN2d,且22MN00。(Ⅰ)求实数,,,abcd的值;(Ⅱ)求直线3yx在矩阵M所对应的线性变换作用下的像的方程。3.(2011福建理科高考)设矩阵baM00(其中a>0,b>0).(I)若a=2,b=3,求矩阵M的逆矩阵M-1;(II)若曲线C:x2+y2=1在矩阵M所对应的线性变换作用下得到曲线C‵:1y4x22,求a,b的值.4.(2012福建理科高考)设曲线12222yxyx在矩阵baA)1(10a对应的变换作用下得到的曲线为122yx。(Ⅰ)求实数ba,的值。(Ⅱ)求2A的逆矩阵。5.(2013福建理科高考)已知直线1:yaxl在矩阵)1021(A对应的变换作用下变为直线1:'byxl(I)求实数ba,的值(II)若点),(00yxP在直线l上,且0000yxyxA,求点P的坐标6.已知矩阵A=[ba01]把点(1,1)变换成点(2,2)(I)求a、b的值(II)求曲线C:x2+y2=1在矩阵A的变换作用下对应的曲线方程。7.已知AOB的三顶点43(0,0),(0,4),(23,2),34OAB设AOB在矩阵所对应的变换作用下得到''AOB,求''OAB和''AOB的面积。8..设是把坐标平面上的点的横坐标伸长到倍,纵坐标伸长到倍的伸压变换.(Ⅰ)求矩阵的特征值及相应的特征向量;(Ⅱ)求逆矩阵以及椭圆22149xy在的作用下的新曲线的方程.9.直线4:1xl先经过矩阵44nmA作用,再经过矩阵1011B作用,变为直线42:2yxl,求矩阵A。10.已知矩阵10102,,:4000ABlxyab矩阵直线经矩阵A所对应的变换得直线l2,直线l2又经矩阵B所对应的变换得到直线3:40lxy,求直线l2的方程。11.已知二阶矩阵13aMd有特征值1及对应的一个特征向量113e.(Ⅰ)求矩阵M;(Ⅱ)设曲线C在矩阵M的作用下得到的方程为2221xy,求曲线C的方程.12.如果曲线2243xxyy1在矩阵11ab的作用下变换得到曲线221xy,求ab的值。设矩阵M所对应的变换是把坐标平面上的点的横坐标伸长到2倍,纵坐标伸长到3倍的伸缩变换.(Ⅰ)求矩阵M的特征值及相应的特征向量;(Ⅱ)求逆矩阵1M以及椭圆22149xy在1M的作用下的新曲线的方程.13.二阶矩阵M对应的变换将点(1,-1)与(-2,1)分别变换成点(-1,-1)与(0,-2).(Ⅰ)求矩阵M;(Ⅱ)设直线l在变换M作用下得到了直线m:2x-y=4,求l的方程14.已知矩阵221aM,其中aR,若点P(1,-2)在矩阵M的变换下得到点'(4,0)P(i)求实数a的值;(ii)求矩阵M的特征值及其对应的特征向量。15.已知矩阵1102M:(1)求矩阵M的逆矩阵1M;(2)求矩阵M的特征值及相应的特征向量16.已知矩阵1214A,向量74(I)求矩阵A的特征值1、2和特征向量1、2;(Ⅱ)求5A的值。17.设矩阵M所对应的变换是把坐标平面上的点的横坐标伸长到2倍,纵坐标伸长到3倍的伸缩变换.(Ⅰ)求矩阵M的特征值及相应的特征向量;(Ⅱ)求逆矩阵1M以及椭圆22149xy在1M的作用下的新曲线的方程.18.已知aR,,矩阵0201,100PQa,若矩阵PQ对应的变换把直线1:40lxy变为直线2:40lxy,求实数a的值。19.已知矩阵10aMc的一个特征值为1,它对应的一个特征向量113e。[来源:学科网ZXXK](Ⅰ)求矩阵M;(Ⅱ)点P(1,1)经过矩阵M所对应的变换,得到点Q,求点Q的坐标。20.已知矩阵11Aab,A的一个特征值2,其对应的特征向量是121.(Ⅰ)求矩阵A;(Ⅱ)求直线2yx在矩阵M所对应的线性变换下的像的方程21.已知矩阵A111a,其中Ra,若点)1,1(P在矩阵A的变换下得到)3,0('P.(1)求实数a的值及A-1;(2)矩阵A的特征值和特征向量..22.已知矩阵1012,0134MN①求二阶矩阵X,使MX=N;②求矩阵X的特征值以及其中一个特征值相应的一个特征向量23.已知矩阵122xM的一个特征值为3,求另一个特征值及其对应的一个特征向量.24.已知矩阵1214A,向量74(I)求矩阵A的特征值1、2和特征向量1、2;(Ⅱ)求5A的值。解:(I)矩阵A的特征多项式为212()5614f令()0f,得122,3,当12时,得121;当23时,得2114分(Ⅱ)由12mn得274mnmn,得3,1mn555512123)3()AAAA(55551122214353()323113997直线4:1xl先经过矩阵44nmA作用,再经过矩阵1011B作用,变为直线42:2yxl,求矩阵A。解法1:设444nmnBAC,则直线1l上的点),(yx经矩阵C变换为直线2l上的点),(''yx,则ynxyymxnx4,)4()4('',代入42''yx,得4)122()83(ymxn与4:1xl比较系数得,3,6nm4364A解法2:设1l经矩阵作用变成直线l,直线l上的点),(yx经矩阵C变换为直线2l上的点),(''yx,则有yyyxx'',,代入42''yx得0432,4)(2yxyyx即再设直线1l上的点),(yx经矩阵A变换为直线l上的点),(''yx,则有ynxymyxx4,4'',代入0432''yx得04)122()83(ymxn与4:1xl比较系数得,3,6nm4364A已知矩阵A=[ba01]把点(1,1)变换成点(2,2)①求a、b的值求曲线C:x2+y2=1在矩阵A的变换作用下对应的曲线方程。(1)解:①由[ba01](11)=(22)得221ba∴a=1,b=2……………………………………………………(3分)②∵A=[2011],对应的坐标变换公式为yyyxx2,,得,,,2121yyyxx代入x2+y2=1得1212,,,2,yyxx∴所求的曲线方程为:12122yxyx……………………(7分)二阶矩阵M对应的变换将点(1,-1)与(-2,1)分别变换成点(-1,-1)与(0,-2).(Ⅰ)求矩阵M;(Ⅱ)设直线l在变换M作用下得到了直线m:2x-y=4,求l的方程解:(Ⅰ)设bdac,则有bdac11=11,bdac21=02,所以120,,122ababcdcd且,……解得1234abcd所以M=1234(Ⅱ)因为1223434xxxyyyxy且m:24xy,



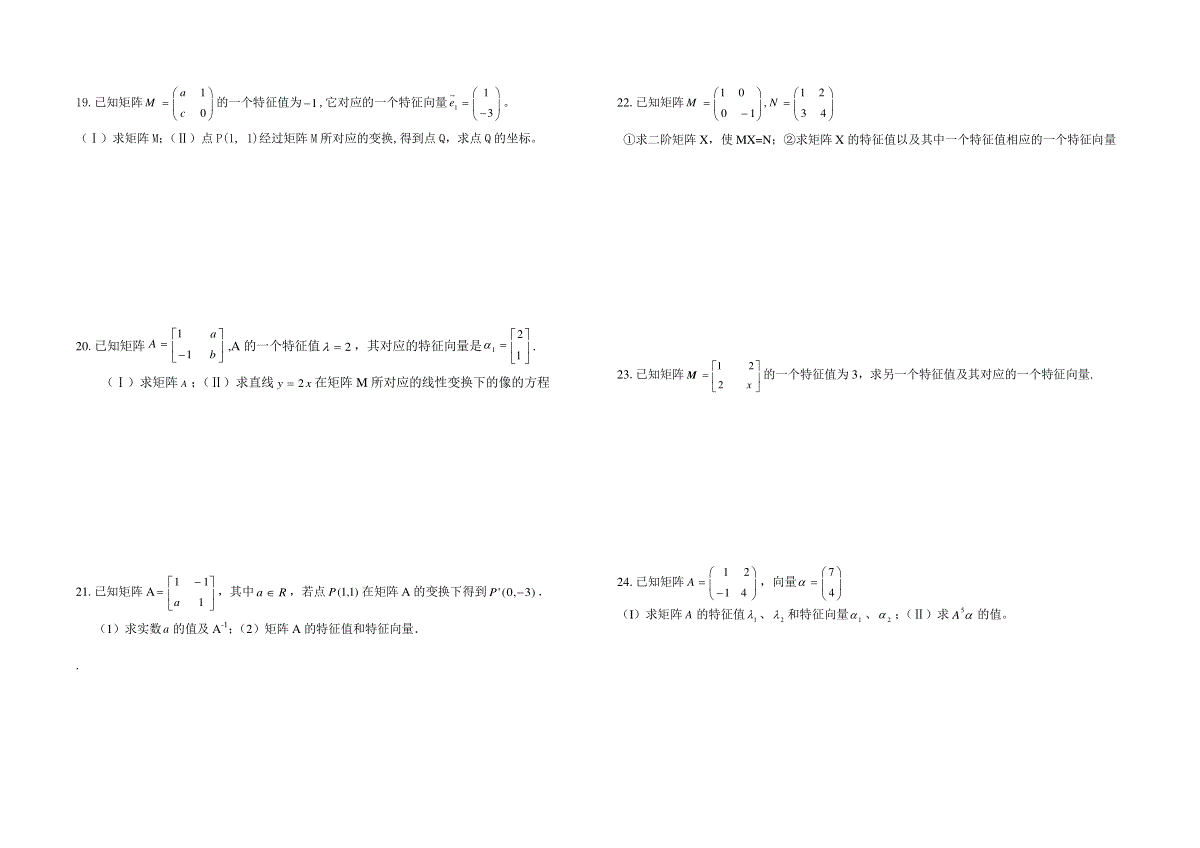
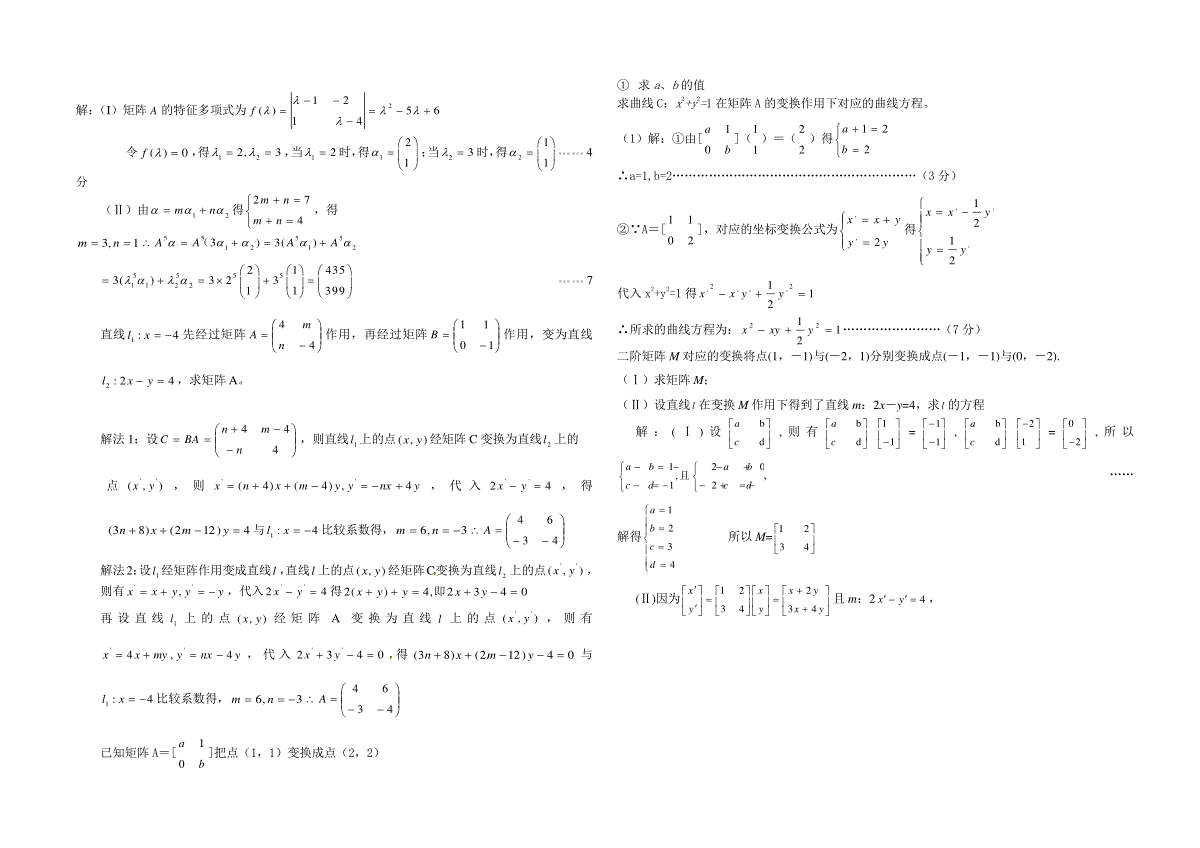
 三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
本文标题:矩阵专题练习doc
链接地址:https://www.777doc.com/doc-2174789 .html