特殊化方法在数学解题中的运用

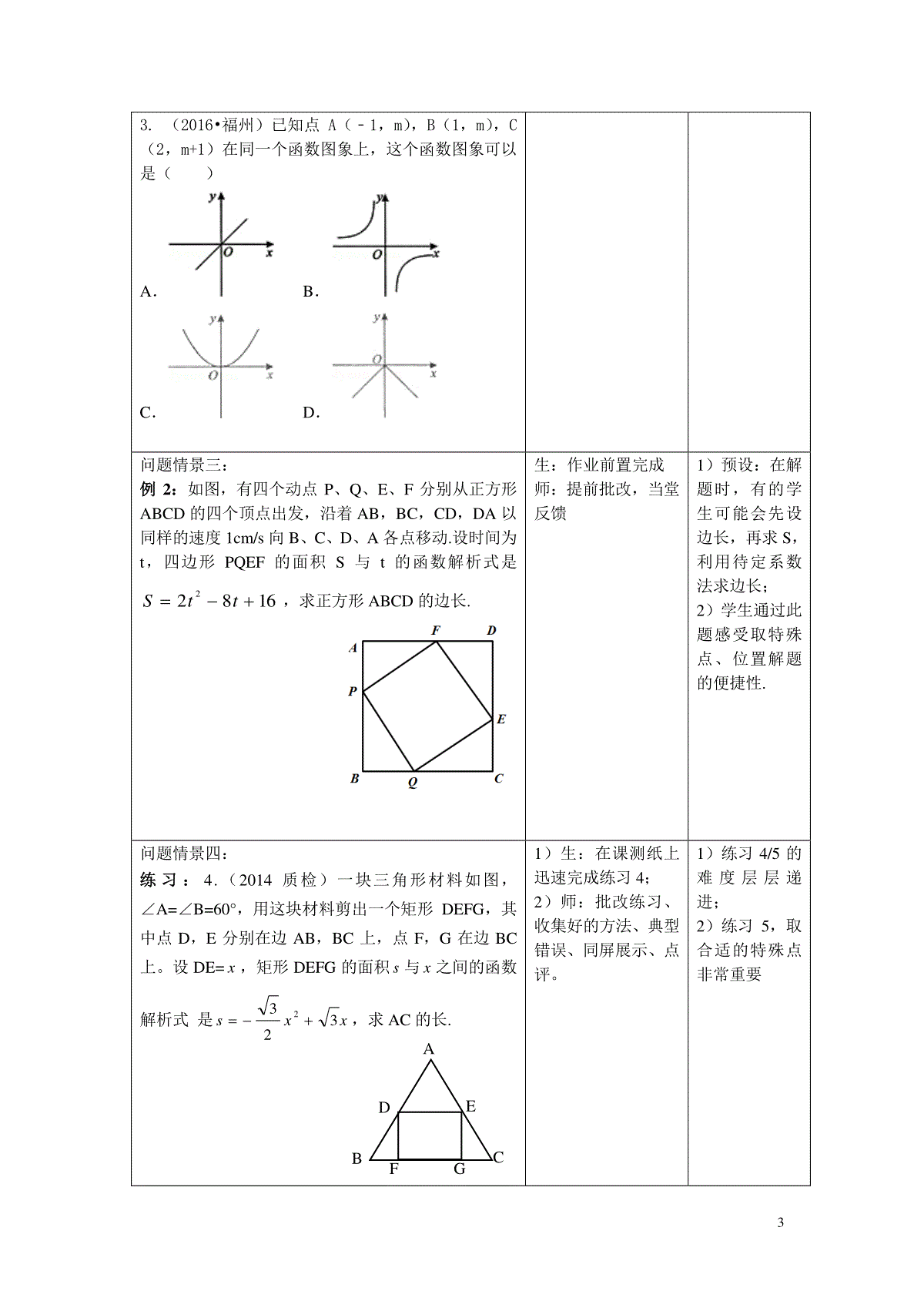
1案例名称2016-2017年九年级中考第二轮专题复习---特殊化方法在数学解题中的运用科目数学教学对象初三5班授课者王虎课时1课型复习课授课时间2017年5月11日一、课标解读“数学基本思想”考查的主要内容数学基本思想着重考查学生对函数与方程思想、数形结合思想、分类与整合思想、特殊与一般思想、化归与转化思想、或然与必然思想等的领悟程度。④特殊与一般思想人们对一类新事物的认识往往是通过对某些个体的认识与研究，逐渐积累对这类事物的了解，逐渐形成对这类事物总体的认识，发现特点，掌握规律，形成共识，由浅入深，由现象到本质，由局部到整体，这种认识事物的过程是由特殊到一般的认识过程。但这并不是目的，还需要用理论指导实践，用所得到的特点和规律解决这类事物中的新问题，这种认识事物的过程是由一般到特殊的认识过程。于是这种由特殊到一般再由一般到特殊反复认识的过程，就是人们认识世界的基本过程之一。数学研究也不例外，这种由特殊到一般，由一般到特殊的研究数学问题的思想，就是数学研究中的特殊与一般思想。二、考情解读普查2016年福建九地市中考卷和2016-2017初三质检考卷，每套都有题目可以运用到特殊化方法。字母取值的特殊化，在选择题中，代入特殊值，结合排除法帮助解题，如厦门市质检考第7题，南平质检第7/9题，福州质检卷第8/10题等；点或图形的特殊化，如厦门2016年质检第16、23题，南平质检第22题等；特殊化方法还可以提供探索、猜想的路径，过渡到一般帮助解题，如：厦门质检第24题等。此外，在解决大题时，特殊化方法还可以作为一种“不完全”的验证方法检验答案是否正确；在最值问题中，取特殊值（均值等）、特殊角、特殊点、特殊形状等帮助解题。如果运用灵活得当，特殊法方法可以在每份试卷中发挥威力、帮助考生解题。三、教学目标（知识，技能，情感态度、价值观）教学目标知识技能1.字母取值得特殊化，对于选择题，会代入特殊值，结合排除法解题2.点或图形位置的特殊化3.几何中角度的定值问题或角度间的数量关系问题，懂得“特殊值探究——猜想——一般化验证”的步骤数学思考领会特殊与一般思想解决问题在不同情境中，学会灵活运用特殊化方法解题情感态度积极思维、克服畏难情绪，发散思维、开拓脑洞重点培养学生在不同问题中，运用特殊化方法帮助解题的意识难点会选择合适的特殊值、特殊点、特殊位置等帮助解题四、教学策略选择与设计在本节课的学案设计中，我选择了“特殊化方法在数学解题中的运用”中的三个内容，主要讲解，其它内容出现在课后练习中作为补充，题目来源基本是九地市2016中考、2016-2017初三质检。教学过程：1.微课讲解特殊法——例题作业前置——提前批改；2.前置作业评讲——当堂练习——学生展示——教师点评；3.评价反馈.2在教学中，让学生亲身体验解题过程，通过对比分析，让学生感受特殊值解题的优越性。五、教学环境及资源准备教室，白板投影、PPT几何画板课件、直尺等日常教学工具六、教学过程教学过程师生行为设计意图及资源准备情景引入：某次考试，同学甲化简式子：2141222xxxxx，得到答案22x，下课后找乙核对答案，同学乙的答案跟他不一样，同学甲忘记了步骤，乙同学没有把题目重新做一遍，就说明了甲同学的答案是错误的，你知道乙是怎么做的吗？启发学生积极思考，举手回答问题由生活情境引入，引导学生思考，了解学生运用特殊化方法的情况．问题情景一：例1：已知抛物线y＝ax2＋bx＋c和y＝max2＋mbx＋mc，其中a，b，c，m均为正数，且m≠1.则关于这两条抛物线，下列判断正确的是（）A.顶点的纵坐标相同B.对称轴相同C.与y轴的交点相同D.其中一条经过平移可以与另一条重合仿照微课讲解，写出分析过程。生：作业前置完成师：提前批改，当堂反馈1）此题参数较多，学生要学会取a、b、c、m为整数0、1这样的特殊值；2）学生通过此题懂得运用特殊值+排除法排除选项，留下正确答案.问题情景二：练习1.若关于x的一元二次方程ax2＋2x－12＝0（a＜0）有两个不相等的实数根，则a的取值范围是（）A.a＜－2B.a＞－2C.－2＜a＜0D.－2≤a＜02．已知432xyz（x、y、z均不为零），则33xyzy的值是（）A．12B．1C．2D．31）生：在课测纸上迅速完成练习1/2/3；2）师：批改组长练习、收集好的方法、典型错误3）生：组长批改学生练习，互相讨论、交流4）生：学生展示5）师：教师点评1）通过生生讨论、交流，让更多学生理解特殊化方法；2）典型错误分析，避免错误运用方法33.（2016•福州）已知点A（﹣1，m），B（1，m），C（2，m+1）在同一个函数图象上，这个函数图象可以是（）A．B．C．D．问题情景三：例2：如图，有四个动点P、Q、E、F分别从正方形ABCD的四个顶点出发，沿着AB，BC，CD，DA以同样的速度1cm/s向B、C、D、A各点移动.设时间为t，四边形PQEF的面积S与t的函数解析式是16822ttS，求正方形ABCD的边长.生：作业前置完成师：提前批改，当堂反馈1）预设：在解题时，有的学生可能会先设边长，再求S，利用待定系数法求边长；2）学生通过此题感受取特殊点、位置解题的便捷性.问题情景四：练习：4.（2014质检）一块三角形材料如图，∠A=∠B=60°，用这块材料剪出一个矩形DEFG，其中点D，E分别在边AB，BC上，点F，G在边BC上。设DE=x，矩形DEFG的面积s与x之间的函数解析式是xxs3232，求AC的长.1）生：在课测纸上迅速完成练习4；2）师：批改练习、收集好的方法、典型错误、同屏展示、点评。1）练习4/5的难度层层递进；2）练习5，取合适的特殊点非常重要ABACADAEAFAGA45.（2016质检）如图，在矩形ABCD中，点E在BC边上，动点P以2厘米/秒的速度从点A出发，沿△AED的边按照A→E→D→A的顺序运动一周.设点P从A出发经x（x＞0）秒后，△ABP的面积是y.已知点E是BC的中点，当点P在线段ED上时，y＝125x；当点P在线段AD上时，y＝32－4x.求矩形的长和宽.问题情境五：例3：如图，AB//CD，BE平分∠ABD，DE平分∠BDC，请问BE⊥ED吗？说明理由.分析：第一步，取特殊角度：设∠DBE=30º，则∠ABD=________，则∠BDC=________，则∠BDE=________，从而∠BED=_________；取另一特殊角：设∠DBE=________º，则∠ABD=________.则∠BDC=________，则∠BDE=________，从而∠BED=_________；第二步，猜想：BE⊥ED________（填“是”或“否”）成立.第三步，一般化：设∠DBE=x，则∠ABD=______________，则∠BDC=________________，则∠BDE=________________，从而∠BED=_________.第四步，得出结论：BE⊥ED.练习6.如图，∠ACB=90°，D、E在AB上且AD=AC，BE=BC，求∠DCE的度数。生：作业前置完成师：提前批改，当堂反馈1）学生在解此题时，很可能用整体法，所以设计成填空的形式，引导学生通过此题了解“特殊化探究——猜想——一般化证明”的过程，并通过练习6实际操作；2）学生要理解为什么不能只取一个特殊角PEDCBA5问题情境六：练习7.（2016质检）在⊙O中，点C在劣弧︵AB上，D是弦AB上的点，∠ACD＝40°.若DC的延长线上存在点P，使得PD＝PB，试探究∠ABC与∠OBP的数量关系，并加以证明.1）生：迅速完成练习7；2）师：收集不同方法、展示、点评如果设一个角为x，则设∠BAC；或设∠ABC与∠OBP两个角，较为复杂课堂小结：1.字母取值得特殊化，对于选择题，可代入特殊值，结合排除法解题2.点或图形位置的特殊化3.几何中角度的定值问题或角度间的数量关系问题，可以用“特殊值探究——猜想——一般化验证”.前置作业：3道例题+练习6；.课堂练习：练习1、2、3、4、5、7课后巩固：练习卷A板书设计：主题：期末专题复习——特殊化方法在数学解题中的运用范例书写区点评修改区白板展示区