2.1圆(2)课件

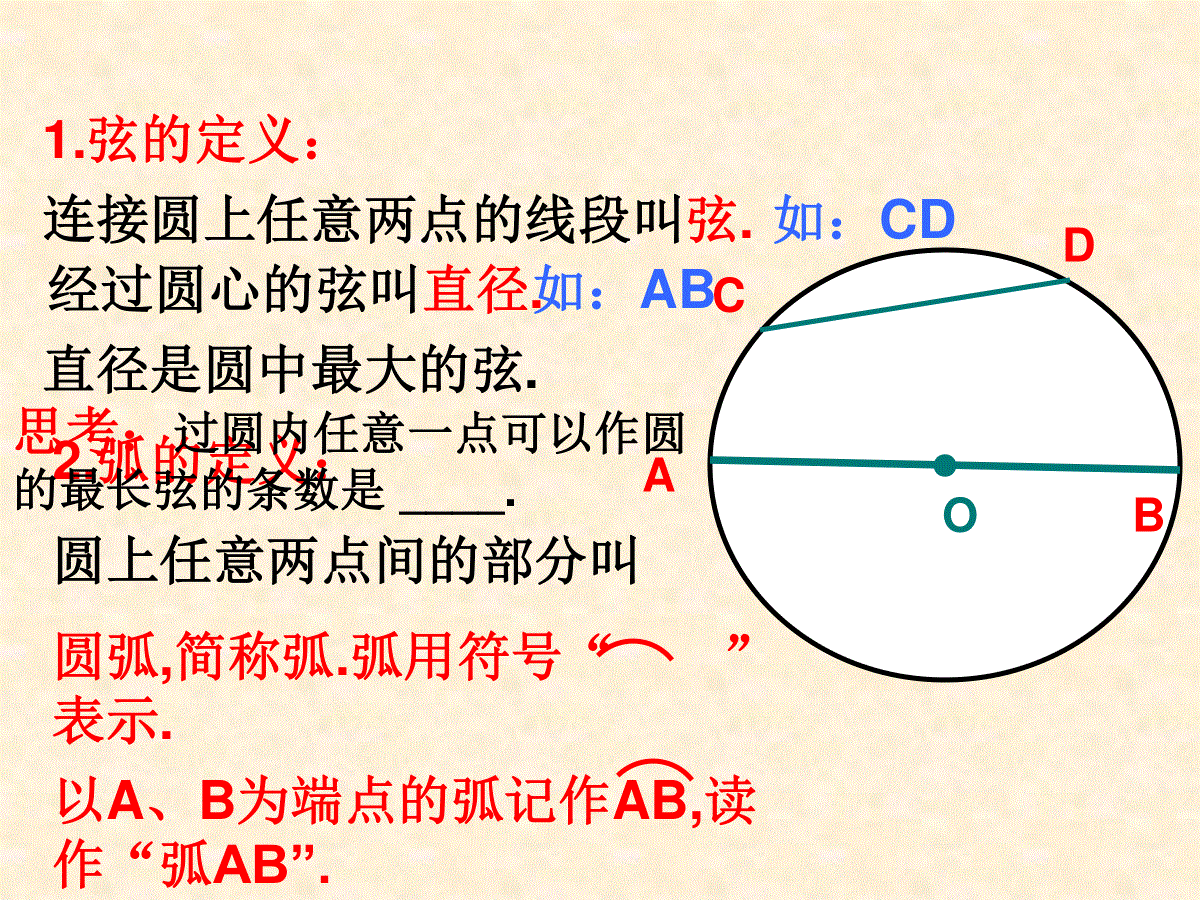
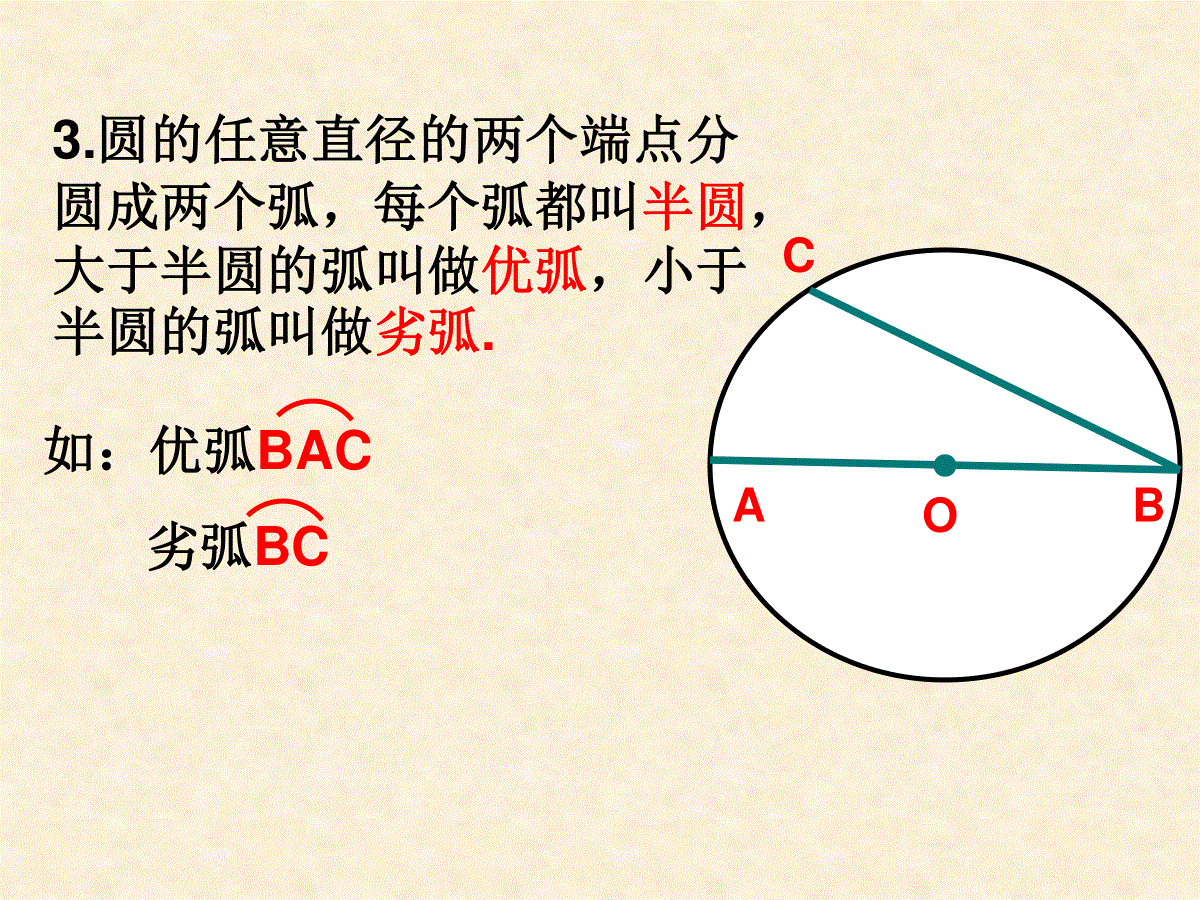
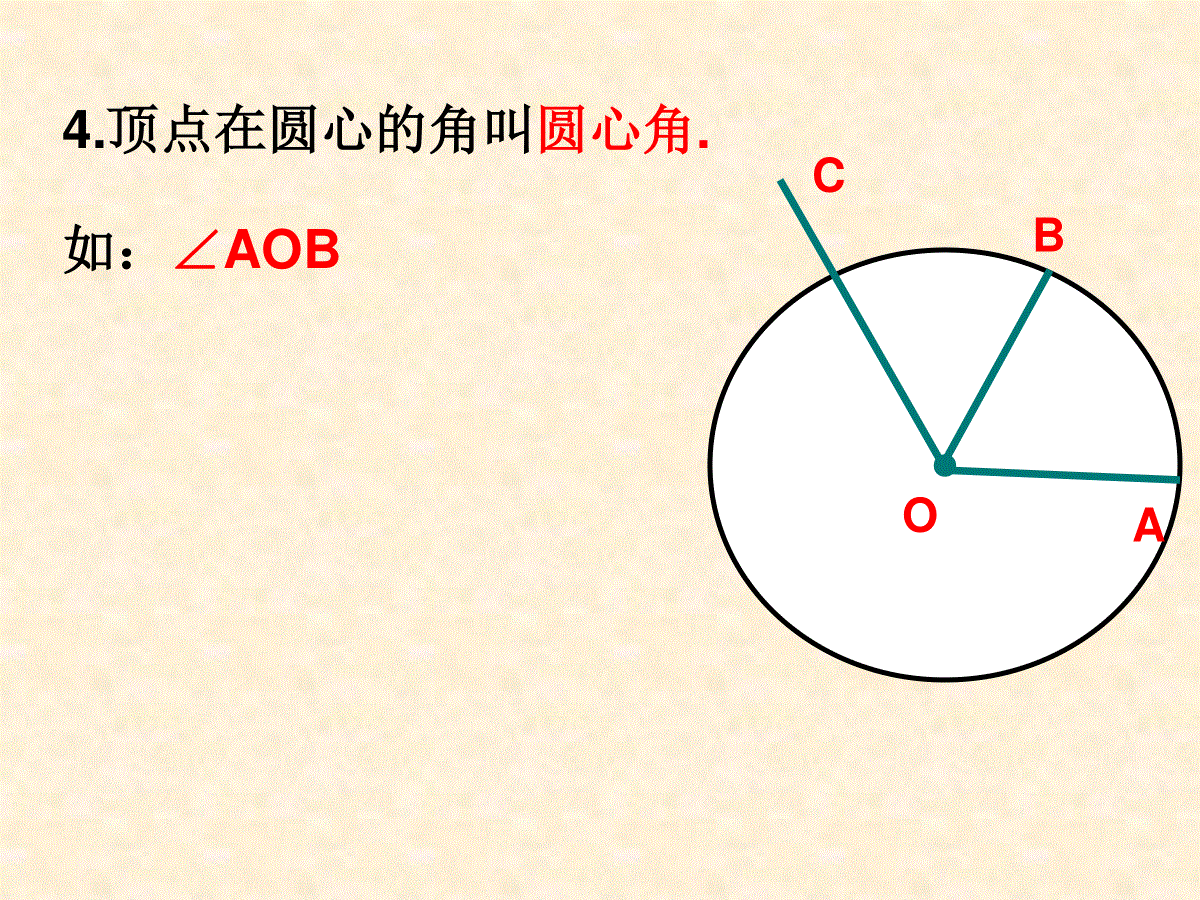
2.1圆（二）●OCDAB连接圆上任意两点的线段叫弦.1.弦的定义：如：CD经过圆心的弦叫直径.圆上任意两点间的部分叫圆弧,简称弧.弧用符号“”表示.以A、B为端点的弧记作AB,读作“弧AB”.如：AB直径是圆中最大的弦.2.弧的定义：思考：过圆内任意一点可以作圆的最长弦的条数是____.●ABCO3.圆的任意直径的两个端点分圆成两个弧，每个弧都叫半圆，大于半圆的弧叫做优弧，小于半圆的弧叫做劣弧.如：优弧BAC劣弧BC4.顶点在圆心的角叫圆心角.●BOA如：∠AOBC5.圆心相同，半径不等的圆叫同心圆.●●O●O2●O16.能够互相重合的两个圆叫等圆◆同圆或等圆的半径相等●●●●BACD在同圆或等圆中，能够互相重合的弧叫等弧考考你的判断力：长度相等的两条弧是等弧吗？●●O例1.如图：点A、B和点C、D分别在两个同心圆上，且∠AOB=∠COD,∠C与∠D相等吗？为什么？ABDC典型例题如图，AB是⊙O的直径，C是BA延长线上一点，点D在⊙O上，且CD=OA，CD的延长线交⊙O于点E.若∠C=20°，求∠BOE的度数.思考与探索：（1）直径是圆中最大的弦.（）（2）长度相等的两条弧是等弧.（）（3）半径相等的两个半圆是等弧.（）（4）面积相等的两个圆是等圆.（）（5）同一条弦所对的两条弧一定是等弧.（）巩固练习1.判断正误：2.下列说法中，正确的是（）A、长度相等的两条弧是等弧B、优弧一定大于劣弧C、不同的圆中不可能有相等的弦D、直径是弦且是同一圆中最长的弦3.如图，在O中，点A,O,D以及点B,O,C分别在同一条直线上，则图中弦的条数是（）A．2条B．3条C．4条D．5条●●●●●ABODC4.如图：点A、B、C、D在⊙O上.在图中画出以这4点中的2点为端点的弦.这样的弦共有多少条？巩固练习●5.（1）在图中，画出⊙O的两条直径（2）依次连接这两条直径的端点，得一个四边形.判断这个四边形的形状，并说明理由.ABCDO巩固练习6.如图，AB是圆O的直径，点C在圆O上，CD⊥AB，垂足为D，已知CD=4，AD=8，求AB的长.巩固练习7.如图，DE为圆O的直径，A为ED延长线一点，过点A的一条直线交圆心O于B,C两点，且AB=OC,∠COE=78°.求∠A的度数.巩固练习8.如图，AB是⊙O的弦，点C、D在AB上，且AC=BD.判断△OCD的形状，并说明理由.巩固练习9.如图，在以点O为圆心的两个同心圆中，大圆的半径OA、OB分别交小圆于点C、D.AB与CD有怎样的位置关系？为什么？巩固练习10.如图，圆O的直径AB=4，半径AB=4，半径OC⊥AB，点D在BC上，DE⊥OC，DF⊥AB，垂足分别为E、F.求EF的长.(图见书P43)巩固练习如图，AB是半圆O的直径，点P从点O出发，沿线段OA－弧AB－线段BO的路径匀速运动一周．设线段OP长为s，运动时间为t，则下列图形能大致刻画与之间关系的是（）矩形ABCD中，AB=8，，点P在边AB上，且BP=3AP，如果圆P是以点P为圆心，PD为半径的圆，那么下列判断正确的是（）A．点B、C均在圆P外B．点B在圆P外、点C在圆P内C．点B在圆P内、点C在圆P外D．点B、C均在圆P内若⊙P的半径长为11，圆心P的坐标为(6，8)，则平面直角坐标系的原点O与⊙P位置关系是()A．在圆内B．在圆外C．在圆上D．无法确定2.已知圆O半径为1，点P到点O的距离为R,关于x的方程x2-2x+R=0有实数根，则点P与圆O的位置关系是_______.3.在数轴上，点A所表示的实数为3，点B所表示的实数为a，⊙A的半径为2，下列说法中不正确的是（）A．当a5时，点B在⊙A内B．当1a5时，点B在⊙A内C．当a1时，点B在⊙A外D．当a5时，点B在⊙A外1.⊙O的半径为4，圆心到点P的距离为d，且d是方程x2－2x－8＝0的根，则点P与⊙O的位置关系是()A、点P在⊙O内部B、点P在⊙O上C、点P在⊙O外部D、点P不在⊙O上复习练习：