当前位置:首页 > 中学教育 > 高中教育 > 必修5第三章不等式练习题及答案ABC卷
数学5(必修)第三章:不等式[基础训练A组]一、选择题1.若02522xx,则221442xxx等于()A.54xB.3C.3D.x452.下列各对不等式中同解的是()A.72x与xxx72B.0)1(2x与01xC.13x与13xD.33)1(xx与xx1113.若122x()142x,则函数2xy的值域是()A.1[,2)8B.1[,2]8C.1(,]8D.[2,)4.设11ab,则下列不等式中恒成立的是()A.ba11B.ba11C.2abD.22ab5.如果实数,xy满足221xy,则(1)(1)xyxy有()A.最小值21和最大值1B.最大值1和最小值43C.最小值43而无最大值D.最大值1而无最小值6.二次方程22(1)20xaxa,有一个根比1大,另一个根比1小,则a的取值范围是()A.31aB.20aC.10aD.02a二、填空题1.若方程2222(1)34420xmxmmnn有实根,则实数m_______;且实数n_______。2.一个两位数的个位数字比十位数字大2,若这个两位数小于30,则这个两位数为________________。3.设函数23()lg()4fxxx,则()fx的单调递减区间是。4.当x______时,函数)2(22xxy有最_______值,且最值是_________。5.若22*1()1,()1,()()2fnnngnnnnnNn,用不等号从小到大连结起来为____________。三、解答题1.解不等式(1)2(23)log(3)0xx(2)2232142xx2.不等式049)1(220822mxmmxxx的解集为R,求实数m的取值范围。3.(1)求yxz2的最大值,使式中的x、y满足约束条件.1,1,yyxxy(2)求yxz2的最大值,使式中的x、y满足约束条件2212516xy4.已知2a,求证:1loglog1aaaa(数学5必修)第三章:不等式[综合训练B组]一、选择题1.一元二次不等式220axbx的解集是11(,)23,则ab的值是()。A.10B.10C.14D.142.设集合等于则BAxxBxxA,31|,21|()A.2131,B.,21C.,,3131D.,,21313.关于x的不等式22155(2)(2)22xxkkkk的解集是()A.12xB.12xC.2xD.2x4.下列各函数中,最小值为2的是()A.1yxxB.1sinsinyxx,(0,)2xC.2232xyxD.21yxx5.如果221xy,则34xy的最大值是()A.3B.51C.4D.56.已知函数2(0)yaxbxca的图象经过点(1,3)和(1,1)两点,若01c,则a的取值范围是()A.(1,3)B.(1,2)C.2,3D.1,3二、填空题1.设实数,xy满足2210xxy,则xy的取值范围是___________。2.若|3,,AxxabababR,全集IR,则ICA___________。3.若121logaxa的解集是11[,]42,则a的值为___________。4.当02x时,函数21cos28sin()sin2xxfxx的最小值是________。5.设,xyR且191xy,则xy的最小值为________.6.不等式组222232320xxxxxx的解集为__________________。三、解答题1.已知集合23(1)23211331|2,|log(9)log(62)2xxxAxBxxx,又2|0ABxxaxb,求ab等于多少?2.函数4522xxy的最小值为多少?3.已知函数22431mxxnyx的最大值为7,最小值为1,求此函数式。4.设,10a解不等式:2log220xxaaa(数学5必修)第三章:不等式[提高训练C组]一、选择题1.若方程05)2(2mxmx只有正根,则m的取值范围是().A.4m或4mB.45mC.45mD.25m2.若aaxxxf12lg)(2在区间]1,(上递减,则a范围为()A.[1,2)B.[1,2]C.1,D.[2,)3.不等式22lglgxx的解集是()A.1(,1)100B.(100,)C.1(,1)100(100,)D.(0,1)(100,)4.若不等式2log0axx在1(0,)2内恒成立,则a的取值范围是()A.1116aB.1116aC.1016aD.1016a5.若不等式201xaxa有唯一解,则a的取值为()A.0B.2C.4D.66.不等式组131yxyx的区域面积是()A.12B.32C.52D.1二、填空题1.不等式122log(21)log(22)2xx的解集是_______________。2.已知0,0,1abab,则12a21b的范围是____________。3.若0,2yx且tan3tan,xy则xy的最大值为________.4.设0x,则函数1)1(2xxy在x=________时,有最小值__________。5.不等式24x0xx的解集是________________。三、解答题1.若函数()log(4)(0,1)aafxxaax且的值域为R,求实数a的取值范围。2.已知△ABC的三边长是,,abc,且m为正数,求证:abcambmcm。3.解不等式:3)61(log2xx4.已知求函数22()()()(02)xxfxeaeaa的最小值。5.设函数1)(2xbaxxf的值域为4,1,求ba,的值。参考答案(数学5必修)第三章[基础训练A组]一、选择题1.C212520,(21)(2)0,22xxxxx,244122212221423xxxxxxx2.B对于A.727,,2xx与727,02xxxx对于C.31,3131xxx或与13x对于D.33)1(xx与xx111,当10x时,xx111不成立3.B122x2421()24xx,221142,230,31,28xxxxxy4.C对于A,B,倒数法则:11,0ababab,要求,ab同号,2111,1bba而,对于22ab的反例:21.1,1.21,0.8,21.6aabb5.B设2221cos,sin,11sin24xyxy6.C令22()(1)2fxxaxa,则(1)0f且(1)0f即220,1030aaaaa二、填空题1.11,22224(1)4(3442)0mmmnn22244210mmnnm,即22(2)(1)0mnm而22(2)(1)0mnm,即221(2)(1)01,2mnmmn且2.13或24设十位数为a,则个位数为2a,*2810230,,1,211aaaaNa或,即13或243.11,2223310,422xxx,递减则12x,∴1122x4.1,,1大224222(2)2(1)1yxxxxx,当21x时,max1y5.)()()(ngnnf222111(),(),()11fngnnnnnnnn三、解答题1.解:(1)22310312310231xxxx或得232xx或,(3,2)(2,)x(2)22222134210132224,,1322250222xxxxxxxxxx2121,6161xxx或(61,21)(21,61)x2.解:2282002(1)940xxmxmxm恒成立,须恒成立当0m时,240x并不恒成立;当0m时,则204(1)4(94)0mmmm得011,42mmm或12m3.解:(1)作出可行域3maxZ;(2)令''5,4xxyy,则'2'2''()()1,104xyzxy,当直线''104zxy和圆'2'2()()1xy相切时116z,max116Z4.证明:21lglg(1)lglg(1)lg(1)loglog1lg(1)lglglg(1)aaaaaaaaaaaaa而222222lg(1)lg(1)lg(1)lglg(1)lg(1)()lg222aaaaaaa即2lglg(1)lg(1)0,aaa而2lg(1)lg0aaa2lglg(1)lg(1)0lglg(1)aaaaa,即1loglog10aaaa1loglog1aaaa参考答案(数学5必修)第三章[综合训练B组]一、选择题1.D方程220axbx的两个根为12和13,121112,,12,2,14323bababaa2.B12112,0,,02xxxxx或3.B225312(1)1,1,222kkkxxx4.D对于A:不能保证0x,对于B:不能保证1sinsinxx,对于C:不能保证22122xx,对于D:31113112yxxx5.D设cos,sin,343cos4sin5sin()5xyxy6.B3,2,2,021,121abcaccaaaabc二、填空题1.,11,2222211,()1,11xxyyyxyxyxy或2.,6232,()230,3,9,36abababababababab|3,,6,AxxabababR,,6ICA3.2111211111log,()(),(),22222aaaaxaxa4.42221cos28sin2cos8sin1()4tan244sin22sincostanxxxxfxxxxxx5.16199()()10102916xyxyxyxyyx6.(1,3)222301313,13(2)(1)01020xxxxxxxxxx三、解答题1.解:23(1)23332122,60,32,3,22xxxxxxxA2290620,13,(1,3)962xxxBxx,(1,2)AB方程20xaxb的两

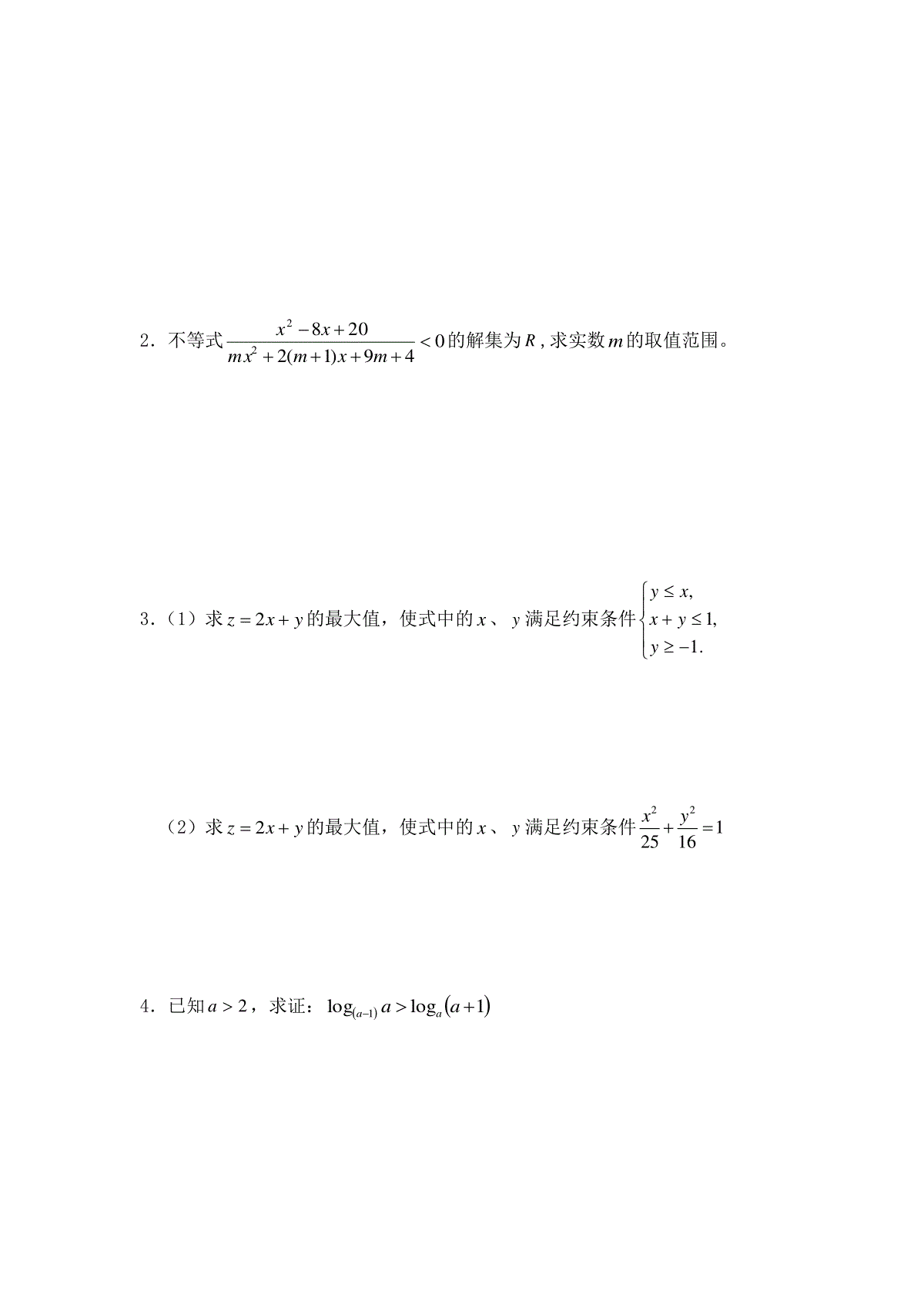
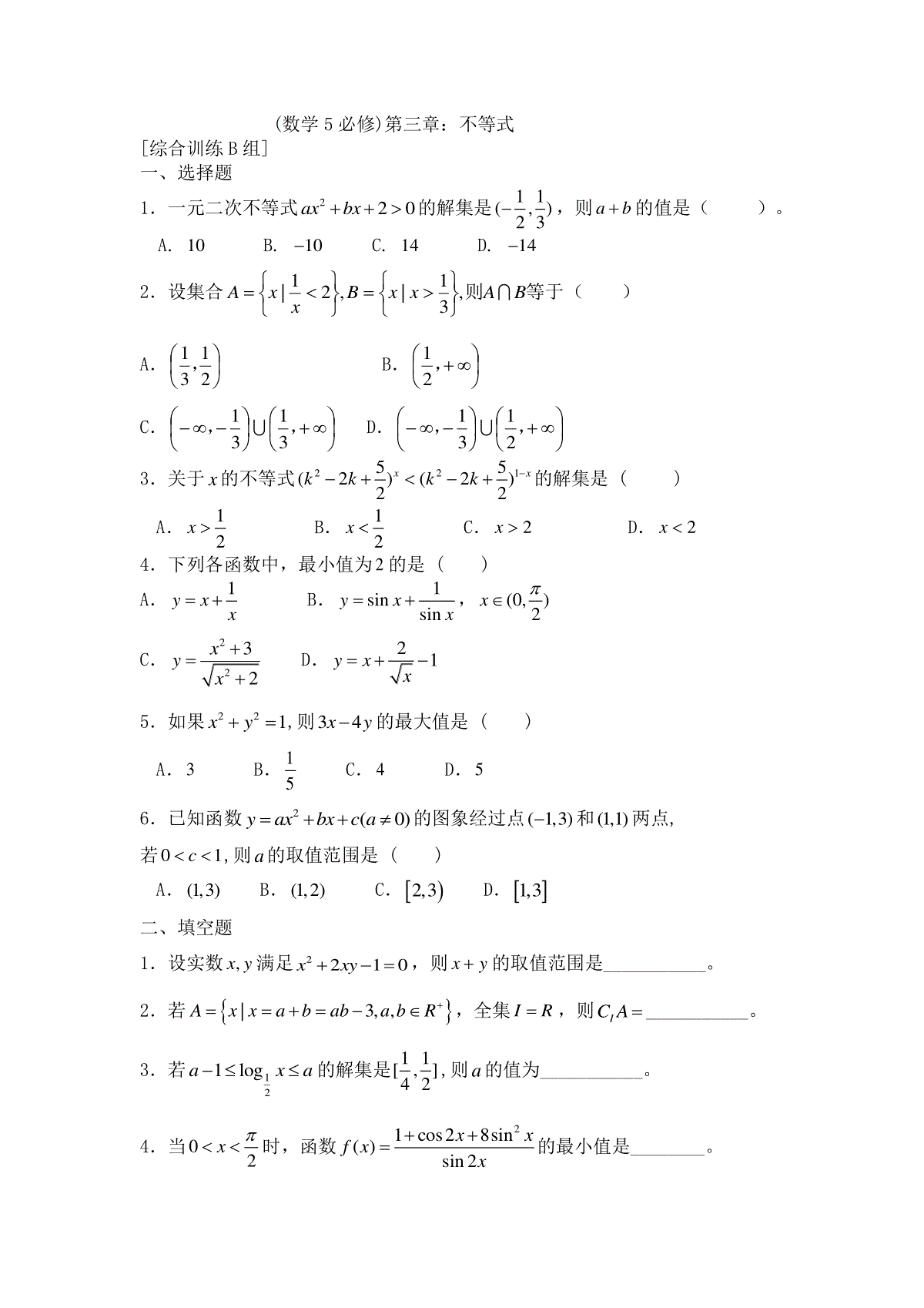


 三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
本文标题:必修5第三章不等式练习题及答案ABC卷
链接地址:https://www.777doc.com/doc-7640886 .html