大学电路理论课程教案-线性直流电路3

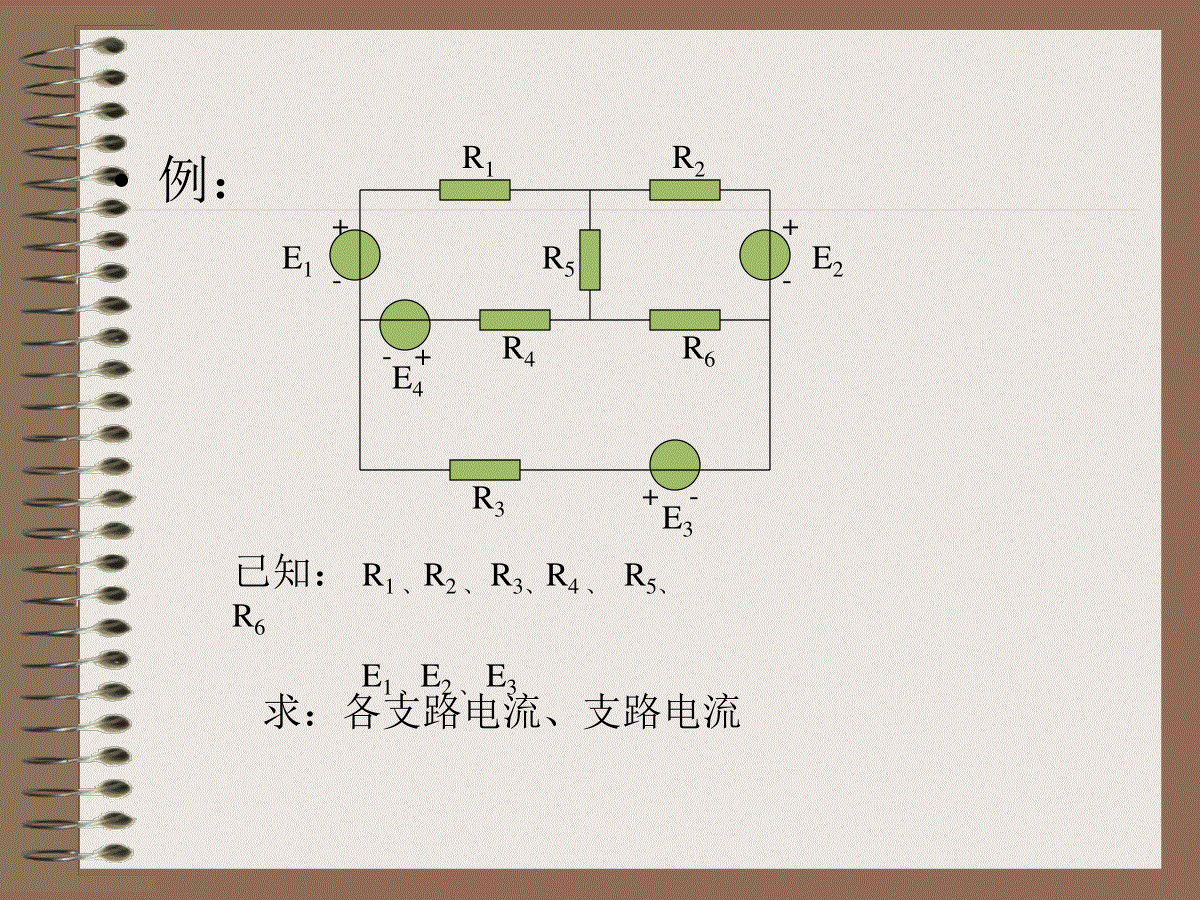
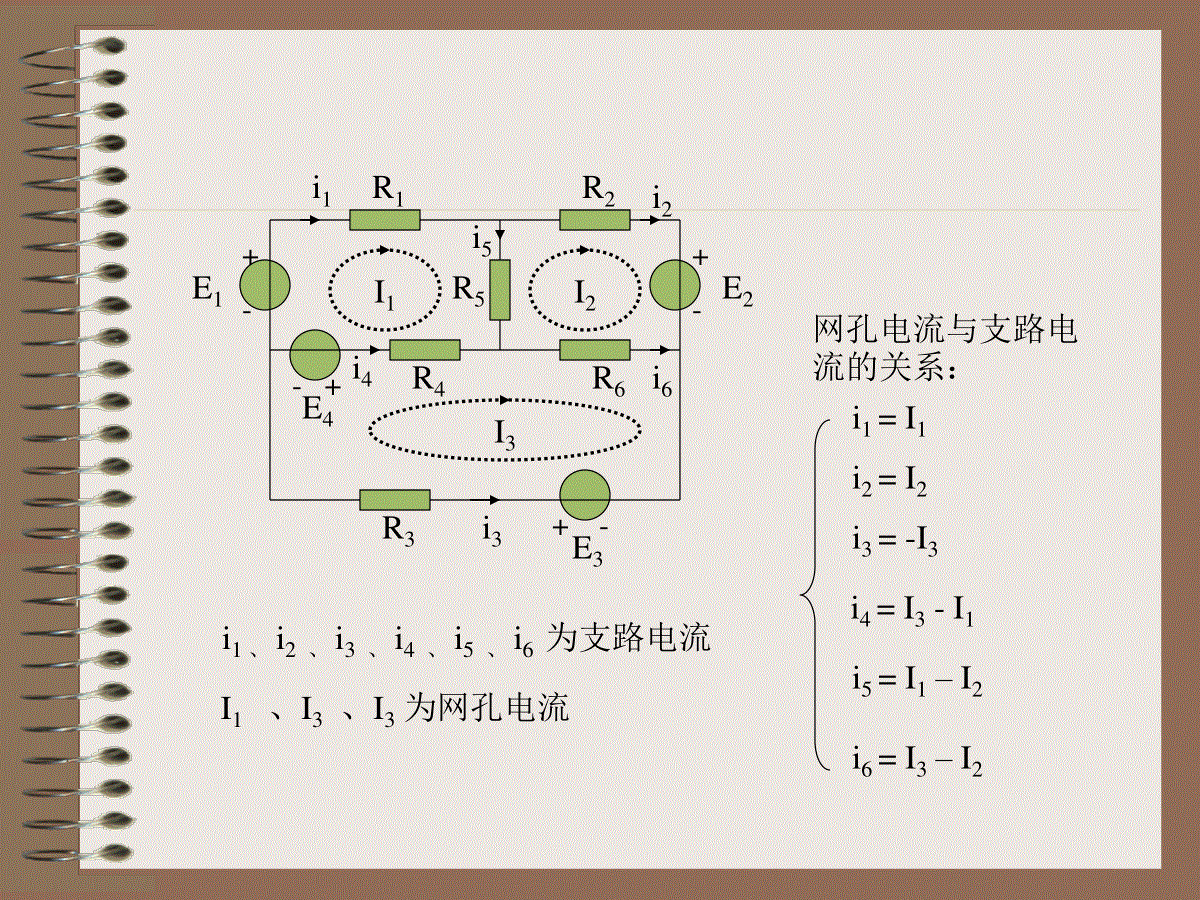
回顾：支路法若电路有b条支路，n个节点求各支路的电压、电流。共2b个未知数各支路的伏安关系方程数b总共方程数2b可列方程数KCL:n-1KVL:b-(n-1)1）支路电流法：以支路电流为求解变量，先列b个方程2）支路电压法：以支路电压为求解变量，先列b个方程•例：R1R2R3R6R4R5E1E2E3+-+-+--+E4已知：R1、R2、R3、R4、R5、R6E1、E2、E3求：各支路电流、支路电流R1R2R3R6R4R5E1E2E3+-+-+--+E4I1I2I3i3i1i5i2i4i6i1=I1i2=I2i3=-I3i4=I3-I1i5=I1–I2i6=I3–I2I1、I3、I3为网孔电流i1、i2、i3、i4、i5、i6为支路电流网孔电流与支路电流的关系：•例：R1R2R3R6R4R5E1E2E3+-+-+--+E4I1I2I3R1I1+R5（I1–I2）+R4（I1–I3）=E1–E4R2I2+R6（I2–I3）+R5（I2–I1）=–E2R3I3+R4（I3–I1）+R6（I3–I2）=E3+E4KVL方程：•例：（R1+R4+R5）I1–R5I2–R4I3=E1–E4–R5I1+（R2+R5+R6）I2–R6I3=–E2–R4I1–R6I2+（R2+R5+R6）I3=E3+E4R1I1+R5（I1–I2）+R4（I1–I3）=E1–E4R2I2+R6（I2–I3）+R5（I2–I1）=–E2R3I3+R4（I3–I1）+R6（I3–I2）=E3+E4合并同类项•例：R1R2R3R6R4R5E1E2E3+-+-+--+E4I1I2I3R1+R4+R5–R5–R4I1=E1–E4–R5R2+R5+R6–R6I2=–E2–R4–R6R3+R4+R6I3=E3+E4网孔分析法•以网孔电流为求解对象，方程数量较少；•列网孔回路的KVL方程•进一步再求各支路电流和电压步骤：1、设网孔电流（顺时针或逆时针方向）2、列KVL方程3、解方程得网孔电流4、由网孔电流求支路电流，进一步求支路电压R1R2I2I1US1R6R5R4R3I3I4I5US3US41234I6+-i1i2i3图3.14R1+R4+R5–R5–R4i1=US1+US4–R5R2+R5+R6–R6i2=0–R4–R6R3+R4+R6i3=US3-US4网孔分析法•例：R3R1R2+-+-E1E2I1I3I2已知：E1=20V、E2=10V、R1=5Ω、R2=10Ω、R3=20Ω求：I1、I2、I325-20i1=20-2030i2=-10i1i2网孔分析法的一些特殊情况1、受控电压源例：图3.16R2R1R3+-+-US1US2I2i1i2+-αU1+-γI2+-U1R1+R2-R2i1US1-αU1-R2R1+R2i2-US2-γI2+αU1=U1=i1R1I2=i1-i2