2020届高三物理一轮复习 第九章 第2讲 磁场对运动电荷的作用课件

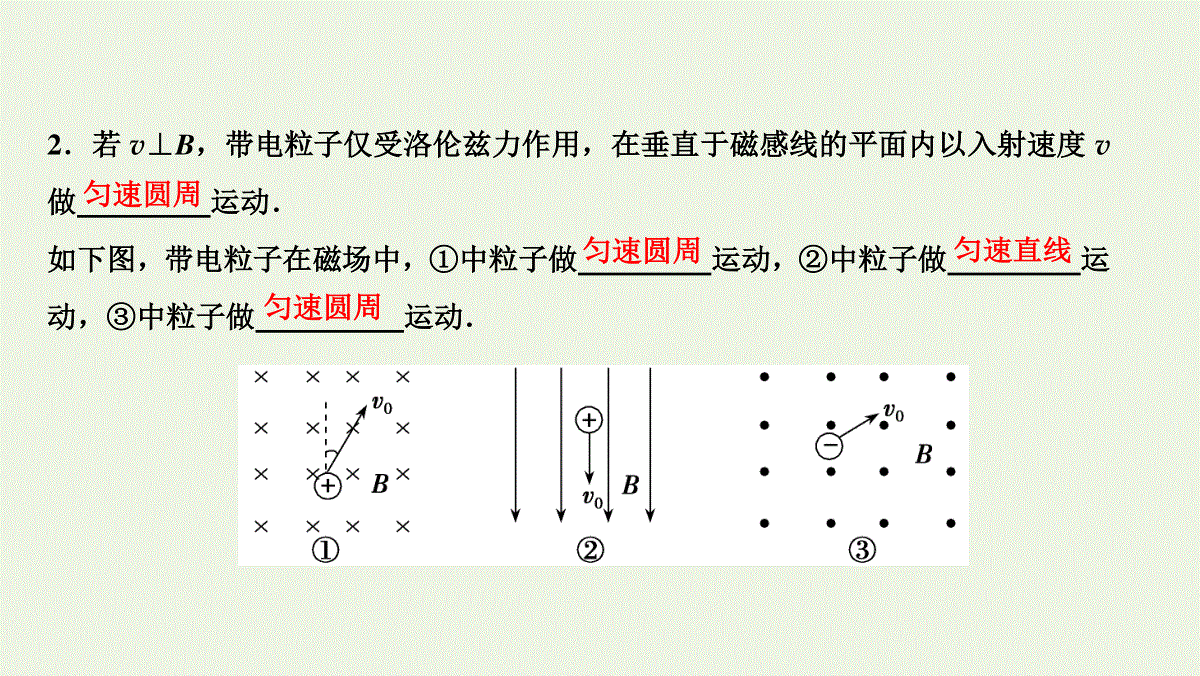
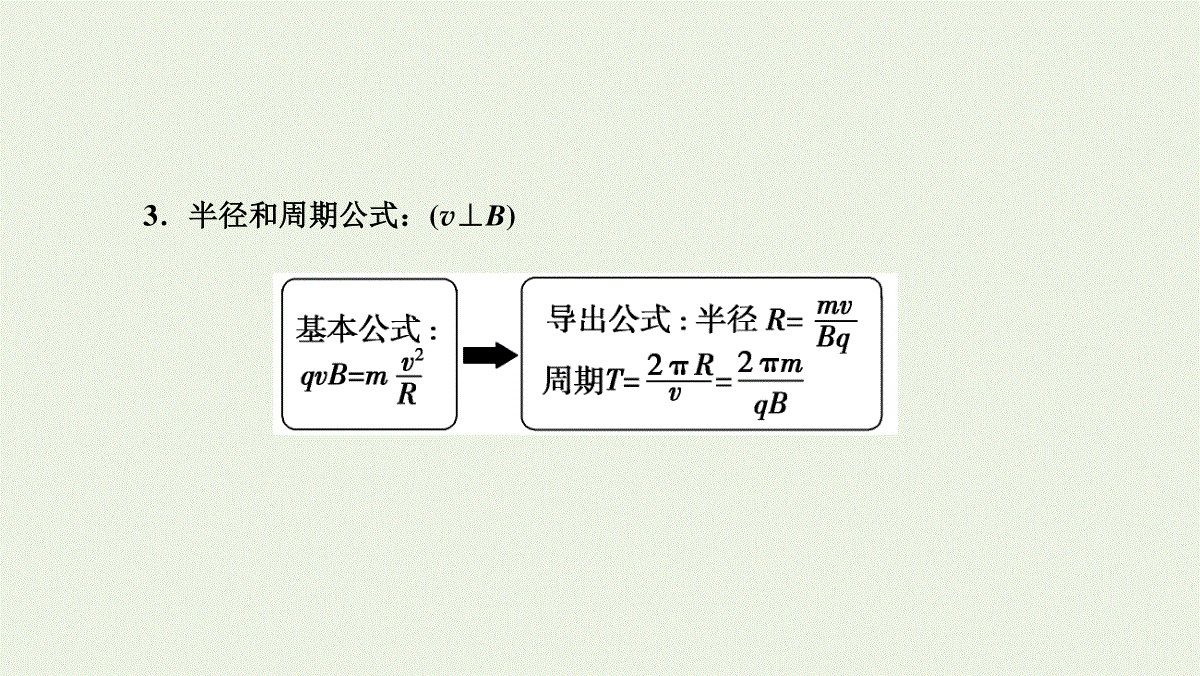
高频考点·分类突破基础知识·自主梳理目录ONTENTSC学科素养提升4课时作业第2讲磁场对运动电荷的作用第九章磁场一、洛伦兹力、洛伦兹力的方向和大小1．洛伦兹力：磁场对的作用力叫洛伦兹力．2．洛伦兹力的方向(1)判定方法：左手定则：掌心——磁感线穿入掌心；四指——指向正电荷运动的方向或负电荷运动的；拇指——指向的方向．(2)方向特点：F⊥B，F⊥v，即F垂直于B和v决定的．运动电荷垂直反方向洛伦兹力平面3．洛伦兹力的大小(1)当v∥B时，洛伦兹力F＝.(θ＝0°或180°)(2)当v⊥B时，洛伦兹力F＝.(θ＝90°)(3)当v＝0时，洛伦兹力F＝0.二、带电粒子在匀强磁场中的运动1．若v∥B，带电粒子不受洛伦兹力，在匀强磁场中做运动．0qvB匀速直线2．若v⊥B，带电粒子仅受洛伦兹力作用，在垂直于磁感线的平面内以入射速度v做运动．如下图，带电粒子在磁场中，①中粒子做运动，②中粒子做运动，③中粒子做运动．匀速圆周匀速圆周匀速直线匀速圆周3．半径和周期公式：(v⊥B)■判一判记一记易错易混判一判(1)洛伦兹力和安培力是性质完全不同的两种力．()(2)洛伦兹力和安培力的方向都与磁场方向垂直．()(3)带电粒子的速度大小相同，所受洛伦兹力不一定相同．()(4)粒子在只受到洛伦兹力作用时运动的动能不变．()×√√√(5)运动电荷进入磁场后(无其他力作用)可能做匀速直线运动．()(6)根据周期公式T＝2πrv得出T与v成反比．()(7)带电粒子在匀强磁场中做匀速圆周运动时，其运动半径与带电粒子的比荷有关．()(8)带电粒子在电场越强的地方受电场力越大，同理带电粒子在磁场越强的地方受磁场力越大．()√×√×规律结论记一记(1)应用带电粒子在磁场中做匀速圆周运动时的半径和周期公式时，一定要写出qvB＝mv2R，不能直接应用R＝mvqB.(2)解决带电粒子在磁场中运动的基本思路：圆心的确定→半径的确定和计算→运动时间的确定．(3)粒子速度垂直于磁场时，做匀速圆周运动：R＝mvqB，T＝2πmqB(周期与速率无关)．(4)带电粒子做匀速圆周运动必须抓住几何条件：①入射点和出射点，两个半径的交点和夹角；②两个半径的交点即轨迹的圆心；③两个半径的夹角等于偏转角，偏转角对应粒子在磁场中运动的时间．考点一对洛伦兹力的理解自主学习型1．洛伦兹力的特点(1)利用左手定则判断洛伦兹力的方向，注意区分正、负电荷．(2)当电荷运动方向发生变化时，洛伦兹力的方向也随之变化．(3)运动电荷在磁场中不一定受洛伦兹力作用．(4)洛伦兹力一定不做功．2．洛伦兹力与安培力的联系及区别(1)安培力是洛伦兹力的宏观表现，二者是相同性质的力，都是磁场力．(2)安培力可以做功，而洛伦兹力对运动电荷不做功．3．洛伦兹力与电场力的比较(1)运动电荷在磁场中且运动方向与磁场不平行时才受到洛伦兹力的作用，电荷只要在电场中就受电场力作用．(2)洛伦兹力任何情况下都不做功，而电场力可能做功，也可能不做功．1．[洛伦兹力的特点]下列关于洛伦兹力的说法中，正确的是()A．只要速度大小相同，所受洛伦兹力就相同B．如果把＋q改为－q，且速度反向，大小不变，则洛伦兹力的大小、方向均不变C．洛伦兹力方向一定与电荷速度方向垂直，磁场方向一定与电荷运动方向垂直D．粒子在只受到洛伦兹力作用下运动的动能、速度均不变因为洛伦兹力的大小不但与粒子速度大小有关，而且与粒子速度的方向有关，如当粒子速度与磁场垂直时F＝qvB，当粒子速度与磁场平行时F＝0.又由于洛伦兹力的方向永远与粒子的速度方向垂直，因而速度方向不同时，洛伦兹力的方向也不同，所以A选项错误．因为＋q改为－q且速度反向，由左手定则可知洛伦兹力方向不变，再由F＝qvB知大小也不变，所以B选项正确．因为电荷进入磁场时的速度方向可以与磁场方向成任意夹角，所以C选项错误．因为洛伦兹力总与速度方向垂直，因此，洛伦兹力不做功，粒子动能不变，但洛伦兹力可改变粒子的运动方向，使粒子速度的方向不断改变，所以D选项错误．B2．[洛伦兹力对运动的影响]如图所示，表面粗糙的绝缘斜面固定于水平地面上，并处于方向垂直纸面向外、磁感应强度为B的匀强磁场(图中未画出)中，质量为m、电荷量为＋Q的小滑块从斜面顶端由静止下滑．在滑块下滑的过程中，下列判断正确的是()A．滑块受到的摩擦力不变B．滑块到达斜面底端时的动能与B的大小无关C．B很大时，滑块最终可能静止于斜面上D．滑块受到的洛伦兹力方向垂直斜面并指向斜面小滑块向下运动的过程中受到重力、垂直斜面向下的洛伦兹力、斜面的支持力和摩擦力，向下运动的过程中，速度增大，洛伦兹力增大，支持力增大，滑动摩擦力增大，选项A错误，D正确；B的大小不同，洛伦兹力的大小不同，导致滑动摩擦力大小不同，根据动能定理，摩擦力做功不同，滑块到达斜面底端的动能不同，选项B错误；滑块之所以开始时能由静止下滑，是因为重力沿斜面向下的分力大于摩擦力，B很大时，滑块一旦运动，不会停止，最终做匀速直线运动，选项C错误．D3．[洛伦兹力对运动的影响](多选)一个带正电的小球沿光滑绝缘的桌面向右运动，速度方向垂直于位于桌子右侧、方向水平向里的匀强磁场，如图所示，小球飞离桌面后落到地板上，设飞行时间为t1，水平射程为x1，着地速度为v1.撤去磁场，其余的条件不变，小球飞行时间为t2，水平射程为x2，着地速度为v2，则下列论述正确的是()A．x1＞x2B．t1＞t2C．v1和v2大小相等D．v1和v2方向相同当桌面右边存在磁场时，由左手定则可知，带正电的小球在飞行过程中受到斜向右上方的洛伦兹力作用，此力在水平方向上的分量向右，竖直分量向上，因此小球水平方向上存在加速度，竖直方向上的加速度a＜g，桌面高度一定，所以t1＞t2，x1＞x2，A、B对；又因为洛伦兹力不做功，故C对；两次小球着地时速度方向不同，D错．ABC考点二带电粒子在匀强磁场中的运动师生互动型1．带电粒子在匀强磁场中的圆周运动分析(1)圆心的确定方法方法一若已知粒子轨迹上的两点的速度方向，则可根据洛伦兹力F⊥v，分别确定两点处速度的垂线，其交点即为圆心，如图(a)；方法二若已知粒子运动轨迹上的两点和其中某一点的速度方向，则可作出此两点的连线(即过这两点的圆弧的弦)的中垂线，中垂线与速度方向的垂线的交点即为圆心，如图(b)．(2)半径的计算方法方法一由物理方法求：半径R＝mvqB；方法二由几何方法求：一般由数学知识(勾股定理、三角函数等)计算来确定．(3)时间的计算方法方法一由圆心角求：t＝θ2π·T；方法二由弧长求：t＝sv.2．带电粒子在不同边界磁场中的运动(1)直线边界(进、出磁场具有对称性，如图所示)(2)平行边界(存在临界条件，如图所示)．(3)圆形边界(沿径向射入必沿径向射出，如图所示)．[典例](多选)(2019·甘肃天水模拟)如图所示，竖直平行线MN、PQ间距离为a，其间存在垂直纸面向里的匀强磁场(含边界PQ)，磁感应强度为B，MN上O处的粒子源能沿不同方向释放比荷为qm的带负电粒子，速度大小相等、方向均垂直磁场．粒子间的相互作用及重力不计，设粒子速度方向与射线OM夹角为θ，当粒子沿θ＝60°射入时，恰好垂直PQ射出，则()A.从PQ边界垂直射出的粒子在磁场中运动的时间为πm6qBB．沿θ＝90°射入的粒子，在磁场中运动的时间最长C．粒子的速率为aqBmD．PQ边界上有粒子射出的长度为23a[思路点拨]解此题关键是根据“恰好垂直PQ射出”“运动的时间最长”“PQ边界上有粒子射出”等条件画出粒子在磁场中的运动轨迹，利用几何关系求解．[解析]带电粒子在磁场中运动，不计重力，则粒子只受洛伦兹力做圆周运动，有Bvq＝mv2R，所以v＝BqRm，粒子沿θ＝60°射入时，恰好垂直PQ射出，则粒子在磁场中转过30°，如图甲所示，所以有Rsin30°＝a，解得R＝2a，故v＝BqRm＝2aqBm，故C错误；t＝30°360°T＝2πR12v＝πR6v＝πm6qB，A正确；θ＝0°时，如图乙所示，粒子离开磁场时在PQ上过O点的水平线上方3a处；当θ增大时，粒子离开磁场时在PQ上的位置下移，直到粒子运动轨迹与PQ相切，θ继续增大，则粒子不能从PQ边界射出；粒子运动轨迹与PQ相切时，由半径R＝2a可知，粒子转过的角度为60°，所以，出射点在O的水平线下方3a处，所以，PQ边界上有粒子射出的长度为23a，D正确；粒子在磁场中做圆周运动的半径相同，周期相同，由D分析可知，粒子出射点在PQ上时，当粒子运动轨迹与PQ相切时，粒子在磁场中运动的圆弧对应的弦最长，粒子转过的角度最大θ1＝120°，如图丙所示；当120°＜θ＜180°时，粒子从MN边界射出，且θ越大，对应的圆心角较小，运动的时间越小，所以，沿θ＝120°射入的粒子，在磁场中运动的时间最长，B错误．[答案]AD[规律方法]带电粒子在磁场中做匀速圆周运动的分析方法1．[带电粒子在直线边界磁场中的运动](2019·陕西渭南模拟)在真空室中，有垂直于纸面向里的匀强磁场，三个质子1、2和3分别以大小相等、方向如图所示的初速度v1、v2和v3经过平板MN上的小孔O射入匀强磁场，这三个质子打到平板MN上的位置到小孔O的距离分别是s1、s2和s3，不计质子重力，则有()A．s1s2s3B．s1s2s3C．s1＝s3s2D.s1＝s3s2由已知条件可知三个质子运动轨迹的半径相等．由于初速度v1和v3的方向与MN的夹角相等，所以这两个质子的运动轨迹正好能组合成一个完整的圆，则这两个质子打到平板MN上的位置到小孔的距离是相等的，且小于轨迹圆的直径；而初速度为v2的质子方向与MN垂直，则它的运动轨迹正好是半圆，所以质子打到平板MN上的位置到小孔的距离恰好是圆的直径，即s1＝s3s2，D正确．D2．[带电粒子在圆形磁场中的运动](2017·高考全国卷Ⅱ)如图，虚线所示的圆形区域内存在一垂直于纸面的匀强磁场，P为磁场边界上的一点，大量相同的带电粒子以相同的速率经过P点，在纸面内沿不同的方向射入磁场．若粒子射入速率为v1，这些粒子在磁场边界的出射点分布在六分之一圆周上．若粒子射入速率为v2，相应的出射点分布在三分之一圆周上．不计重力及带电粒子之间的相互作用，则v2∶v1为()A.3∶2B.2∶1C.3∶1D．3∶2根据作图分析可知，当粒子在磁场中运动半个圆周时，打到圆形磁场边界的位置距P点最远，则当粒子射入的速率为v1，轨迹如图甲所示，设圆形磁场半径为R，由几何知识可知，粒子运动的轨道半径为r1＝Rcos60°＝12R；若粒子射入的速率为v2，轨迹如图乙所示，由几何知识可知，粒子运动的轨道半径为r2＝Rcos30°＝32R.根据轨道半径公式r＝mvqB可知，v2∶v1＝r2∶r1＝3∶1，故选项C正确．C3．[带电粒子在多边界磁场中的运动]如图所示，正六边形abcdef区域内有垂直于纸面的匀强磁场．一带正电的粒子从f点沿fd方向射入磁场区域，当速度大小为vb时，从b点离开磁场，在磁场中运动的时间为tb，当速度大小为vc时，从c点离开磁场，在磁场中运动的时间为tc.不计粒子重力．则()A．vb∶vc＝1∶2，tb∶tc＝2∶1B．vb∶vc＝2∶1，tb∶tc＝1∶2C．vb∶vc＝2∶1，tb∶tc＝2∶1D．vb∶vc＝1∶2，tb∶tc＝1∶2如图所示，设正六边形的边长为l，当带电粒子的速度大小为vb时，其圆心在a点，轨道半径r1＝l，转过的圆心角θ1＝23π；当带电粒子的速率为vc时，其圆心在O点(即fa、cb延长线的交点)，故轨道半径r2＝2l，转过的圆心角θ2＝π3.根据qvB＝mv2r，得v＝qBrm，故vbvc＝r1r2＝12.又T＝2πrv，则T＝2πmqB，所以两粒子在磁场中做圆周运动的周期相等，又t＝θ2πT，所以tbtc＝θ1θ2＝21.故选项A正确，选项B、C、D错误．A4.[带电粒子在连续磁场中的运动]如图所示，在无限长的竖直边界AC和DE间，上、下部分分别充满方向垂直于ADEC平面向外的匀强磁场，上部分区域的磁感应强度大小为B0，OF为上、下