泉州市2020届高三5月质检(理科数学)试题word版

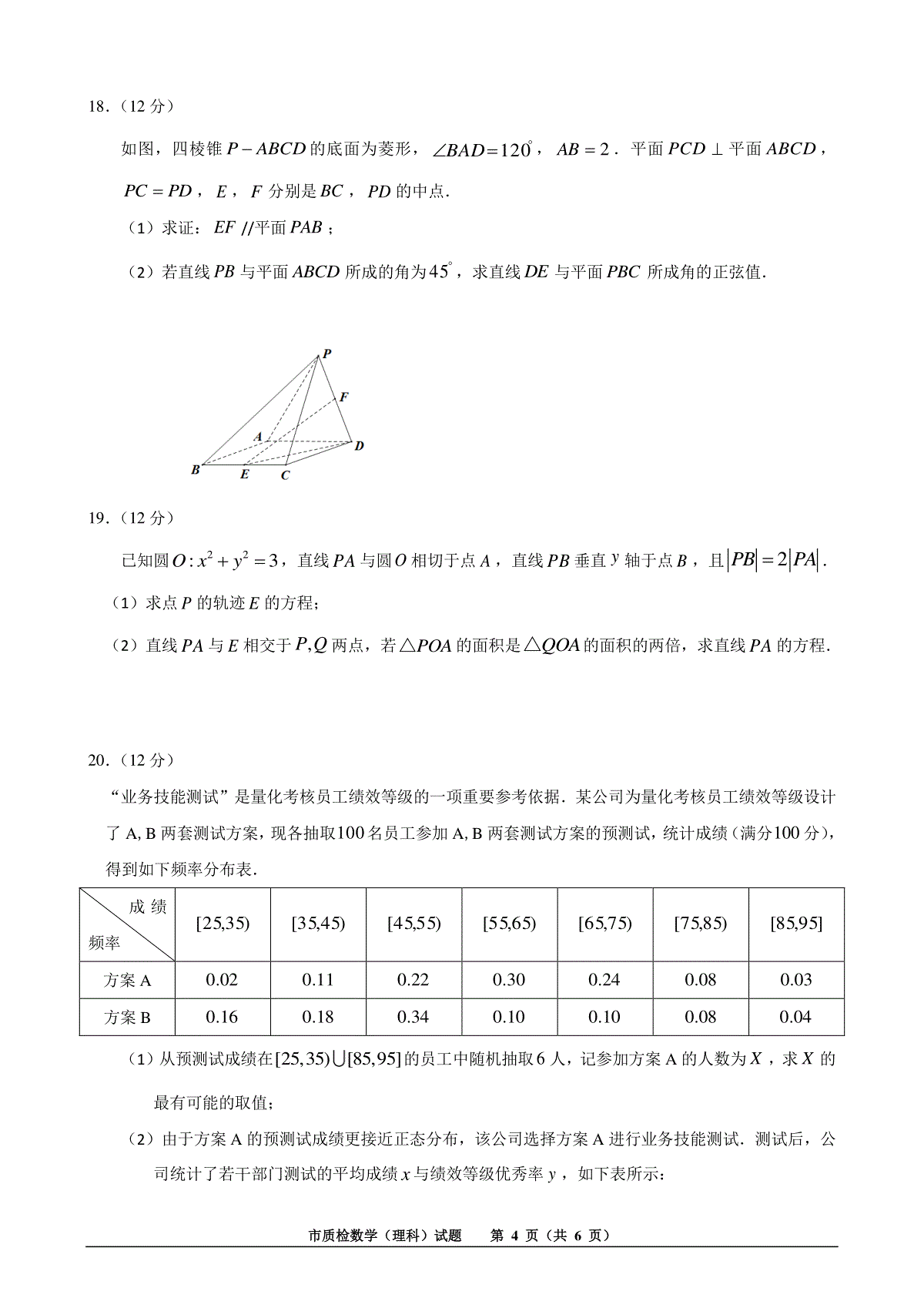
市质检数学（理科）试题第1页（共6页）准考证号________________姓名________________（在此卷上答题无效）保密★启用前泉州市2020届普通高中毕业班第二次质量检查理科数学2020.5本试卷共23题，满分150分，共5页．考试用时120分钟．注意事项：1．答题前，考生先将自己的姓名、准考证号填写在答题卡上．2．考生作答时，将答案答在答题卡上．请按照题号在各题的答题区域（黑色线框）内作答，超出答题区域书写的答案无效．在草稿纸、试题卷上答题无效．3．选择题答案使用2B铅笔填涂，如需改动，用橡皮擦干净后，再选涂其它答案标号；非选择题答案使用5.0毫米的黑色中性（签字）笔或碳素笔书写，字体工整、笔迹清楚．4．保持答题卡卡面清洁，不折叠、不破损．考试结束后，将本试卷和答题卡一并交回．一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合10Axx≥，2210Bxxx≤，则ABA．(,1]B．1[1,]2C．1[,1]2D．1[,)22．7(1)(2)xx的展开式中6x的系数为A．14B．28C．70D．983．已知向量2,1AB,4,2AC，则ABC△的面积为A．5B．10C．25D．504．平面直角坐标系中，角的顶点与原点重合，始边与x轴的非负半轴重合，终边过点(3,4)M，则sin(2)A．725B．725C．2425D．24255．音乐与数学有着密切的联系，我国春秋时期有个著名的“三分损益法”：以“宫”为基本音，“宫”经过一次“损”，频率变为原来的23，得到“徵”；“徵”经过一次“益”，频率变为原来的43，得到“商”；……．依市质检数学（理科）试题第2页（共6页）次损益交替变化，获得了“宫、徵、商、羽、角”五个音阶．据此可推得A．“宫、商、角”的频率成等比数列B．“宫、徵、商”的频率成等比数列C．“商、羽、角”的频率成等比数列D．“徵、商、羽”的频率成等比数列6．函数2ln1fxxkx（）的图象不可能是A．xyO1B．xyO1C．xyO1D．xyO17．已知2(sin2)a，sin22b，12log(sin2)c，则A．bcaB．bacC．abcD．cba8．如图，网格纸上小正方形的边长为１，粗实线画出的是某几何体的三视图，其中俯视图是等边三角形，则该几何体的外接球的表面积为A．10B．283C．9D．2539．每年的台风都对泉州地区的渔业造成较大的经济损失．某保险公司为此开发了针对渔船的险种，并将投保的渔船分为I，II两类，两类渔船的比例如图所示．经统计，2019年I，II两类渔船的台风遭损率分别为15%和5%．2020年初，在修复遭损船只的基础上，对I类渔船中的20%进一步改造．保险公司预估这些经过改造的渔船2020年的台风遭损率将降为3%，而其他渔船的台风遭损率不变．假设投保的渔船不变，则下列叙述中正确的是A．2019年投保的渔船的台风遭损率为10%B．2019年所有因台风遭损的投保的渔船中，I类渔船所占的比例不超过80%C．预估2020年I类渔船的台风遭损率会小于II类渔船的台风遭损率的两倍D．预估2020年经过进一步改造的渔船因台风遭损的数量少于II类渔船因台风遭损的数量10．已知双曲线E的左、右焦点分别为21,FF，左、右顶点分别为NM,．点P在E的渐近线上，120PFPF，3MPN，则E的离心率为A．315B．213C．35D．13市质检数学（理科）试题第3页（共6页）11．若0，函数()3sin4cosfxxx（3x0≤≤）的值域为4,5，则cos()3的取值范围是A．71,25B．7,125C．73,255D．74,25512．以,,,,ABCDE为顶点的多面体中，ACCB，ADDB，AEEB，10AB，6CD，则该多面体的体积的最大值为A．303B．80C．90D．503二、填空题：本大题共4小题，每小题5分，共20分．将答案填在答题卡的相应位置．13．在复平面中，复数12,zz对应的点分别为121,2,2,1ZZ．设1z的共轭复数为1z，则12zz_______．14．已知点1,0A，1,0B，过A的直线与抛物线24yx相交于,PQ两点．若P为AQ中点，则PBQB_______．15．ABC△中，角,,ABC所对的边分别为,,abc，AbBacos3sin，3a．若点D在边BC上，且2BDDC，则AD的最大值是_______．16．若存在过点(1,)2a的直线l与函数()exfxx，()eaxgxx的图象都相切，则a_______．三、解答题：共70分．解答应写出文字说明，证明过程或演算步骤．第17～21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．（一）必考题：共60分．17．（12分）记nS为数列na的前n项和，且21a，nnanS)1(2．（1）求nS；（2）若+11=nnnnabSS，数列nb的前n项和为nT，证明：21nT．市质检数学（理科）试题第4页（共6页）18．（12分）如图，四棱锥ABCDP的底面为菱形，120BAD，2AB．平面PCD平面ABCD，PDPC，E，F分别是BC，PD的中点．（1）求证：EF//平面PAB；（2）若直线PB与平面ABCD所成的角为45，求直线DE与平面PBC所成角的正弦值．19．（12分）已知圆22:3Oxy，直线PA与圆O相切于点A，直线PB垂直y轴于点B，且2PBPA．（1）求点P的轨迹E的方程；（2）直线PA与E相交于,PQ两点，若POA△的面积是QOA△的面积的两倍，求直线PA的方程．20．（12分）“业务技能测试”是量化考核员工绩效等级的一项重要参考依据．某公司为量化考核员工绩效等级设计了A,B两套测试方案，现各抽取100名员工参加A,B两套测试方案的预测试，统计成绩（满分100分），得到如下频率分布表．成绩频率)35,25[)45,35[)55,45[)65,55[)75,65[)85,75[]95,85[方案A02.00.1122.00.3024.008.00.03方案B16.018.034.010.010.008.004.0（1）从预测试成绩在[25,35)[85,95]的员工中随机抽取6人，记参加方案A的人数为X，求X的最有可能的取值；（2）由于方案A的预测试成绩更接近正态分布，该公司选择方案A进行业务技能测试．测试后，公司统计了若干部门测试的平均成绩x与绩效等级优秀率y，如下表所示：市质检数学（理科）试题第5页（共6页）x32415468748092y28.034.044.058.066.074.094.0根据数据绘制散点图，初步判断，选用xye作为回归方程．令yzln，经计算得642.0z，7172210.02iiiiixznxzxnx，9.115.0ln．（ⅰ）若某部门测试的平均成绩为60，则其绩效等级优秀率的预报值为多少？（ⅱ）根据统计分析，大致认为各部门测试平均成绩),(~2Nx，其中近似为样本平均数x，2近似为样本方差2s，求某个部门绩效等级优秀率不低于78.0的概率为多少？参考公式与数据：（1）2.132.3ln，66.12.5ln，20s．（2）线性回归方程ˆˆˆybxa中，1221ˆniiiniixynxybxnx，ˆˆaybx．（3）若随机变量),(~2NX，则6826.0)(XP，9544.0)22(XP，9974.0)33(XP．21．（12分）已知函数2211()()ln24fxxaxxxax．（1）若()fx在(0,)单调递增，求a的值；（2）当13e44a时，设函数()()fxgxx的最小值为()ha，求函数()ha的值域．（二）选考题：共10分．请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分．22．［选修4—4：坐标系与参数方程］（10分）直角坐标系xOy中，圆1C:2cos,2sinxy（为参数）上的每一点的横坐标不变，纵坐标变为原来的21，得到曲线2C．以坐标原点O为极点，x轴正半轴为极轴建立极坐标系，直线l的极坐标方程为市质检数学（理科）试题第6页（共6页）cossin24．（1）求2C的普通方程和l的直角坐标方程；（2）设l与两坐标轴分别相交于BA,两点，点Q在2C上,求QAB△的面积的最大值．23．［选修4—5：不等式选讲］（10分）已知函数()23fxxxmx．（1）当1m时，求不等式()8fx≤的解集；（2）当01m≤时，证明：()3fx≥．